Funciones, Ejemplo: Estimar el número π

A continuación escribiremos la primera función.

Existen diversos métodos de estimar el número π, entre estos, series de Taylor, la fórmula de Madhava, Euler, Wallis y el algoritmo de John Machin. Más detalles.

Los ejemplos presentados se basan en Julia for Pythonistas

Uno de los sencillos de implementar es usando la sucesión: \(π = 4 \times \left(1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \dfrac{1}{9}-\dfrac{1}{11}+\dots\right)\)

function estimate_pi(n)
    s = 1.0
    println(n)
    for i in 1:n
        s += (isodd(i) ? -1 : 1) / (2i + 1)
    end
    4s
end

# Nótese que _ se usa como separador de miles
p = estimate_pi(100_000_000)
println("El valor estimado de π ≈ $p")

# El valor de pi es una constante bajo el símbolo o carácter unicode π
# Es equivalente a pi o \pi
println("El error es $(p - π)")

# PI es un número Irracional
println(pi)
println(typeof(pi))
println(typeof(π))

100000000
El valor estimado de π ≈ 3.141592663589326
El error es 9.999532757376528e-9
π
Irrational{:π}
Irrational{:π}

Código Similar en Python

import math

def estimate_pi(n):
    s = 1.0
    for i in range(1, n + 1):
        s += (-1 if i % 2 else 1) / (2 * i + 1)
    return 4 * s

p = estimate_pi(100_000_000)

# f-strings está disponible a partir de la versión 3.6 de Python
print(f"El valor estimado de π ≈ {p}")
print(f"El error es {p - math.pi}")

Diferencias Sutiles

Julia	Python
function	def
for i in X    ...end	for i in X:    ...
1:n	range(1, n+1)
cond ? a : b	a if cond else b
2i + 1	2 * i + 1
4s	return 4 * s
println(a, b)	print(a, b, sep="")
print(a, b)	print(a, b, sep="", end="")
"$p"	f"{p}"
"$(p - π)"	f"{p - math.pi}"

Otras consideraciones

• La identación en Julia no tiene relevancia sintáctica, esta se recomienda para que el código sea legible.

• Los bloques en julia terminan con end.

• Julia puede ser más conciso en su sintaxis, por ejemplo: 4 * s se puede definir también como 4s.

• No es necesario importar muchas de las características matemáticas, por ejemplo, pi o π.

• La palabra clave return es opcional. Se retorna el último valor de la última expresión (4s en el ejemplo).

• Julia permite trabajar directamente con simbolos Unicode como π. También se puede definir a mediante un nombre de variable (ejemplo, π == pi).

Obtener Símbolos Unicode

Es posible obtenerlos a partir de su representación en latex. Tabla de símbolos latex

#Obtener Simbolos Unicode
using REPL.REPLCompletions: latex_symbols, emoji_symbols

println(latex_symbols["\\pi"])
println(latex_symbols["\\theta"])
println(latex_symbols["\\in"])

π
θ
∈

emoji_symbols["\\:smiley:"]

"😃"

• También se pueden consultar en el notebook escribiendo el código latex entre dobe signo de $.

\[\hat{y}\]

# En Julia
r = 10
𝑦̂ = 23 + 5r
println("El valor estimado de y es: ", 𝑦̂)

El valor estimado de y es: 73

• En Python es similar, las dos diferencias son:

1. No podemos usar 5r, este se define como 5*r.

2. println no existe en python, se usa print.

r = 10
𝑦̂ = 23 + 5*r
print("El valor estimado de y es: ", 𝑦̂)

Funciones Genéricas

f(x,y)= x + y

f (generic function with 1 method)

f(10, 8)

18

miFuncion(x, z) = 20 + 2x - 3z

miFuncion (generic function with 1 method)

miFuncion(5, 2)

24

# Análogo a g(x,y) = x * y

function g(x,y)
    return x * y
end

g (generic function with 1 method)

g(10,20)

200

Ejecutar Código Python en Julia

# Importamos el paquete para installar paquetes
using Pkg
# Instalamos el paquete para llamar codigo Python
Pkg.add("PyCall")

   Updating registry at `C:\Users\Fernan\.julia\registries\General`
  Resolving package versions...
  Installed PyCall ─ v1.92.1
Updating `C:\Users\Fernan\.julia\environments\v1.5\Project.toml`
  [438e738f] + PyCall v1.92.1
Updating `C:\Users\Fernan\.julia\environments\v1.5\Manifest.toml`
  [438e738f] + PyCall v1.92.1
   Building PyCall → `C:\Users\Fernan\.julia\packages\PyCall\BcTLp\deps\build.log`

# Importamos el módulo
using PyCall

# Versión de python instalada
sys = pyimport("sys")
sys.version

"3.8.5 (default, Sep  3 2020, 21:29:08) [MSC v.1916 64 bit (AMD64)]"

#Usar codigo Python
py"""
import math

def estimate_pi(n):
    s = 1.0
    for i in range(1, n + 1):
        s += (-1 if i % 2 else 1) / (2 * i + 1)
    return 4 * s

p = estimate_pi(100_000_000)
print(f"El Valor estimado de π es ≈ {p}")
print(f"El error is {p - math.pi}")
"""

El Valor estimado de π es ≈ 3.141592663589326
El error is 9.999532757376528e-09

# Usar un valor calculado de Python
valorde = py"p"
trespi = 3valorde
println("3π es ", trespi)

3π es 9.424777990767979

# Usar numpy
np = pyimport("numpy")
a = np.random.rand(2, 3)

2×3 Array{Float64,2}:
 0.348598  0.0904924  0.484818
 0.8055    0.615658   0.605433

#Usar valores de Julia en Python
exp_a = np.exp(a)

py"""
import numpy as np

result = np.log($exp_a)
"""

println(py"result")

[0.3485976896130741 0.09049244210949274 0.4848177585126648; 0.8055003764177291 0.6156579814071617 0.605433270653951]

# Instalación de PyPlot
using Pkg
Pkg.add("PyPlot")

   Updating registry at `C:\Users\Fernan\.julia\registries\General`
  Resolving package versions...
No Changes to `C:\Users\Fernan\.julia\environments\v1.5\Project.toml`
No Changes to `C:\Users\Fernan\.julia\environments\v1.5\Manifest.toml`

# En Julia se puede usar Matplotlib `pyimport("matplotlib")`
# pero se recomienda usar PyPlot por razones de rendimiento
# PyPlot se basa en matplotlib
using PyPlot

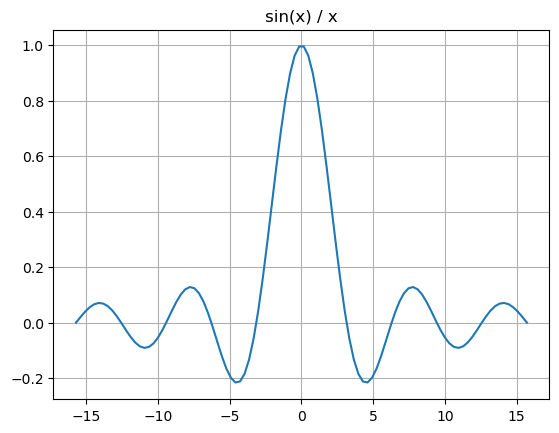
x = range(-5π, 5π, length=100)
plt.plot(x, sin.(x) ./ x)
plt.title("sin(x) / x")
plt.grid("True")
plt.show()

sys:1: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.