Apriori en Python¶
10 min | Última modificación: Junio 28, 2019.
A continuación se presenta una implementación simple del algoritmo Apriori en Python, como complemento a la implementación presentada en R.
[3]:
##
## Preparación
##
from apyori import apriori
import pandas as pd
[8]:
##
## Se preparan los datos
##
data = [['x1', 'x2', 'x3'],
['x1', 'x3'],
['x2', 'x4'],
['x1', 'x2', 'x3'],
['x1', 'x2', 'x5'],
['x1', 'x2', 'x3', 'x4'],
['x4', 'x6'],
['x1', 'x2', 'x4', 'x6'],
['x1', 'x3', 'x4'],
['x1', 'x2', 'x3']]
data
[8]:
[['x1', 'x2', 'x3'],
['x1', 'x3'],
['x2', 'x4'],
['x1', 'x2', 'x3'],
['x1', 'x2', 'x5'],
['x1', 'x2', 'x3', 'x4'],
['x4', 'x6'],
['x1', 'x2', 'x4', 'x6'],
['x1', 'x3', 'x4'],
['x1', 'x2', 'x3']]
[19]:
transactions_rules = apriori(data,
min_support=0.006,
min_confidence=0.25,
min_lift=1,
min_length=1)
transactions_rules = list(transactions_rules)
[20]:
print(len(transactions_rules))
17
[23]:
for item in transactions_rules:
print(item)
RelationRecord(items=frozenset({'x1'}), support=0.8, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x1'}), confidence=0.8, lift=1.0)])
RelationRecord(items=frozenset({'x2'}), support=0.7, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x2'}), confidence=0.7, lift=1.0)])
RelationRecord(items=frozenset({'x3'}), support=0.6, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x3'}), confidence=0.6, lift=1.0)])
RelationRecord(items=frozenset({'x4'}), support=0.5, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x4'}), confidence=0.5, lift=1.0)])
RelationRecord(items=frozenset({'x1', 'x2'}), support=0.6, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x1'}), items_add=frozenset({'x2'}), confidence=0.7499999999999999, lift=1.0714285714285714), OrderedStatistic(items_base=frozenset({'x2'}), items_add=frozenset({'x1'}), confidence=0.8571428571428572, lift=1.0714285714285714)])
RelationRecord(items=frozenset({'x3', 'x1'}), support=0.6, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x1'}), items_add=frozenset({'x3'}), confidence=0.7499999999999999, lift=1.2499999999999998), OrderedStatistic(items_base=frozenset({'x3'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x5', 'x1'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x5'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x5', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x5'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286)])
RelationRecord(items=frozenset({'x6', 'x4'}), support=0.2, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4'}), items_add=frozenset({'x6'}), confidence=0.4, lift=2.0), OrderedStatistic(items_base=frozenset({'x6'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0)])
RelationRecord(items=frozenset({'x3', 'x1', 'x2'}), support=0.4, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x1', 'x2'}), items_add=frozenset({'x3'}), confidence=0.6666666666666667, lift=1.1111111111111114), OrderedStatistic(items_base=frozenset({'x3', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x5', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x5', 'x1'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286), OrderedStatistic(items_base=frozenset({'x5', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x6', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x6', 'x1'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286), OrderedStatistic(items_base=frozenset({'x6', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x4', 'x3', 'x1'}), support=0.2, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x1'}), items_add=frozenset({'x3'}), confidence=0.6666666666666667, lift=1.1111111111111114), OrderedStatistic(items_base=frozenset({'x4', 'x3'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x6', 'x4', 'x1'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x1'}), items_add=frozenset({'x6'}), confidence=0.33333333333333337, lift=1.6666666666666667), OrderedStatistic(items_base=frozenset({'x6', 'x1'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0)])
RelationRecord(items=frozenset({'x6', 'x4', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x2'}), items_add=frozenset({'x6'}), confidence=0.33333333333333337, lift=1.6666666666666667), OrderedStatistic(items_base=frozenset({'x6', 'x2'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0)])
RelationRecord(items=frozenset({'x4', 'x3', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x3', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
RelationRecord(items=frozenset({'x6', 'x4', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x1', 'x2'}), items_add=frozenset({'x6'}), confidence=0.5, lift=2.5), OrderedStatistic(items_base=frozenset({'x6', 'x1', 'x2'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0), OrderedStatistic(items_base=frozenset({'x6', 'x4', 'x1'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286), OrderedStatistic(items_base=frozenset({'x6', 'x4', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
[43]:
for item in transactions_rules:
pair = item[0]
items = [x for x in pair]
print(item)
print(items)
RelationRecord(items=frozenset({'x1'}), support=0.8, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x1'}), confidence=0.8, lift=1.0)])
['x1']
RelationRecord(items=frozenset({'x2'}), support=0.7, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x2'}), confidence=0.7, lift=1.0)])
['x2']
RelationRecord(items=frozenset({'x3'}), support=0.6, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x3'}), confidence=0.6, lift=1.0)])
['x3']
RelationRecord(items=frozenset({'x4'}), support=0.5, ordered_statistics=[OrderedStatistic(items_base=frozenset(), items_add=frozenset({'x4'}), confidence=0.5, lift=1.0)])
['x4']
RelationRecord(items=frozenset({'x1', 'x2'}), support=0.6, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x1'}), items_add=frozenset({'x2'}), confidence=0.7499999999999999, lift=1.0714285714285714), OrderedStatistic(items_base=frozenset({'x2'}), items_add=frozenset({'x1'}), confidence=0.8571428571428572, lift=1.0714285714285714)])
['x1', 'x2']
RelationRecord(items=frozenset({'x3', 'x1'}), support=0.6, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x1'}), items_add=frozenset({'x3'}), confidence=0.7499999999999999, lift=1.2499999999999998), OrderedStatistic(items_base=frozenset({'x3'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x3', 'x1']
RelationRecord(items=frozenset({'x5', 'x1'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x5'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x5', 'x1']
RelationRecord(items=frozenset({'x5', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x5'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286)])
['x5', 'x2']
RelationRecord(items=frozenset({'x6', 'x4'}), support=0.2, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4'}), items_add=frozenset({'x6'}), confidence=0.4, lift=2.0), OrderedStatistic(items_base=frozenset({'x6'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0)])
['x6', 'x4']
RelationRecord(items=frozenset({'x3', 'x1', 'x2'}), support=0.4, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x1', 'x2'}), items_add=frozenset({'x3'}), confidence=0.6666666666666667, lift=1.1111111111111114), OrderedStatistic(items_base=frozenset({'x3', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x3', 'x1', 'x2']
RelationRecord(items=frozenset({'x5', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x5', 'x1'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286), OrderedStatistic(items_base=frozenset({'x5', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x5', 'x1', 'x2']
RelationRecord(items=frozenset({'x6', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x6', 'x1'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286), OrderedStatistic(items_base=frozenset({'x6', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x6', 'x1', 'x2']
RelationRecord(items=frozenset({'x4', 'x3', 'x1'}), support=0.2, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x1'}), items_add=frozenset({'x3'}), confidence=0.6666666666666667, lift=1.1111111111111114), OrderedStatistic(items_base=frozenset({'x4', 'x3'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x4', 'x3', 'x1']
RelationRecord(items=frozenset({'x6', 'x4', 'x1'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x1'}), items_add=frozenset({'x6'}), confidence=0.33333333333333337, lift=1.6666666666666667), OrderedStatistic(items_base=frozenset({'x6', 'x1'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0)])
['x6', 'x4', 'x1']
RelationRecord(items=frozenset({'x6', 'x4', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x2'}), items_add=frozenset({'x6'}), confidence=0.33333333333333337, lift=1.6666666666666667), OrderedStatistic(items_base=frozenset({'x6', 'x2'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0)])
['x6', 'x4', 'x2']
RelationRecord(items=frozenset({'x4', 'x3', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x3', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x4', 'x3', 'x1', 'x2']
RelationRecord(items=frozenset({'x6', 'x4', 'x1', 'x2'}), support=0.1, ordered_statistics=[OrderedStatistic(items_base=frozenset({'x4', 'x1', 'x2'}), items_add=frozenset({'x6'}), confidence=0.5, lift=2.5), OrderedStatistic(items_base=frozenset({'x6', 'x1', 'x2'}), items_add=frozenset({'x4'}), confidence=1.0, lift=2.0), OrderedStatistic(items_base=frozenset({'x6', 'x4', 'x1'}), items_add=frozenset({'x2'}), confidence=1.0, lift=1.4285714285714286), OrderedStatistic(items_base=frozenset({'x6', 'x4', 'x2'}), items_add=frozenset({'x1'}), confidence=1.0, lift=1.25)])
['x6', 'x4', 'x1', 'x2']
[ ]:
[ ]:
[ ]:
[ ]:
[4]:
##
## arules lee un archivo en formato CSV.
## Se crea un archivo con los datos del
## problema planteado
##
data <- paste(
"x1, x2, x3",
"x1, x3",
"x2, x4",
"x1, x2, x3",
"x1, x2, x5",
"x1, x2, x3, x4",
"x4, x6",
"x1, x2, x4, x6",
"x1, x3, x4",
"x1, x2, x3",
sep="\n")
## Se imprime en pantalla para verificar
cat(data)
## Se escribe el archivo en disco duro
write(data, file = "data/apriori.csv")
x1, x2, x3
x1, x3
x2, x4
x1, x2, x3
x1, x2, x5
x1, x2, x3, x4
x4, x6
x1, x2, x4, x6
x1, x3, x4
x1, x2, x3
[ ]:
[ ]:
[ ]:
Objetivos de aprendizaje¶
Al finalizar este tutorial, usted estará en capacidad de:
Explicar que es un conjunto de ítems.
Explicar que es una regla de asociación y cómo se aplica en sistemas de recomendación.
Describir las componentes del algoritmo Apriori.
Explicar los conceptos de lift, support y confidence.
Encontrar a mano las reglas de asociación para un conjunto pequeño de transacciones.
Definición del problema real¶
Un problema típico de los retailers es poder recomendar productos afines a sus compradores basados en el histórico general de las ventas. Estas recomendaciones tienen como fin sugerirle al usuario productos que podría haber olvidado y que usualmente se llevan juntos, o nuevos productos sustitutos que reemplazarían productos ya posicionados. Esta recomendación se basa en el histórico general de la tienda (productos que todas las personas usualmente llevan juntos) y no en las preferencias individuales de los clientes.
Definición del problema en términos de los datos¶
Para ejemplificar el proceso de construcción de las reglas de inducción, se tiene un conjunto ficticio de 10 transacciones realizadas sobre seis posibles ítems (\(x_1, ..., x_6)\), donde cada fila representa una transacción:
# Productos
--------------------
1 x1, x2, x3
2 x1, x3
3 x2, x4
4 x1, x2, x3
5 x1, x2, x5
6 x1, x2, x3, x4
7 x4, x6
8 x1, x2, x4, x6
9 x1, x3, x4
10 x1, x2, x3
El problema consiste en derivar un conjunto de reglas de asociación que permita recomenda un grupo de productos a partir de los productos que ya seleccionó el cliente. Por ejemplo, si un cliente compra \(x_1\) y \(x_3\), ¿qué producto o productos se le deben recomendar?
Solución¶
Transacción¶
Una transacción se representa a través del conjunto de ítems comprados en ella. Así, una transacción con cuatro ítems se representa como:
El problema descrito equivale a determinar los productos \(x_i\), con \(x_i \notin \{x_1, x_2, x_3, x_4 \}\), con mayor probabilidad de ser comprados sabiendo que el cliente ya seleccionó \(x_1\), \(x_2\), \(x_3\) y \(x_4\). Dicho de otra forma, se deben computar las probabilidades condicionales \(\text{Pr}(x_i \, | \, x_1, x_2, x_3, x_4)\) y recomendar los \(N\) productos \(x_i\) con mayor probabilidad condicional de compra. En este problema se asume que SI existe una dependencia entre la compra de un producto y otro; si esta dependencia no existe, no tiene sentido construir el sistema de recomendación.
Regla de asociación¶
De esta forma, el objetivo del sistema de recomendación es construir una regla de asociación de la forma:
la cual indica que cuando se compran \(x_2\), \(x_3\) y \(x_4\) también se compra (implica) \(x_1\).
Es posible evaluar todas las posibles reglas por fuerza bruta (enumeración). Para el caso anterior, las reglas podrían ser: \(\{x_2\} \rightarrow x_1\), \(\{x_3\} \rightarrow x_1\), \(\{x_4\} \rightarrow x_1\), \(\{x_1\} \rightarrow x_2\), \(\{x_3\} \rightarrow x_2\), …, \(\{x_2, x_3\} \rightarrow x_1\), \(...\), \(\{x_1, x_2\} \rightarrow x_4\) y así sucesivamente, hasta construir todas las permutaciones posibles. Sin embargo, esta solución resulta imposible en términos prácticos debido a que la cantidad de reglas crece exponencialmente.
Ejercicio.– ¿Cuántas reglas posibles hay para el caso anterior?
Algoritmo Apriori¶
El algoritmo Apriori se basa en evaluar solamente las reglas que tienen una frecuencia alta (mayor probabilidad). El algoritmo se basa en la siguiente heurística: para que el conjunto \(\{x_1, x_2\}\) sea frecuente (que tenga una probabilidad alta), los ítems \(x_1\) y \(x_2\) deben ser frecuentes; es decir, si \(x_1\) o \(x_2\) son infrecuentes, su combinación no es evaluada.
Para medir la importancia de una regla se usa el soporte y la confianza. Si una regla de asocación se escribe como
el soporte es la proporción de veces que \(X\) aparece respecto al total de transacciones; nótese que acá se está hablando explícitamente de probabilidad.
La confianza se define como:
la cual se interpreta como la cantidad de veces en que la presencia de \(X\) resulta en la presencia de \(Y\). Es decir, ya que se dio \(X\) que tan probable es que se de \(Y\).
Actividad.– Responda la siguiente pregunta: ¿Es verdad que \(\text{confidence}(X \rightarrow Y) = \text{confidence}(Y \rightarrow X)\)?
El algoritmo Apriori opera en dos fases: En la primera fase se identifican todos los conjuntos de ítems que cumplen con el soporte mínimo requerido (o probabilidad mínima de compra). En la segunda fase, con los ítems identificados en la fase uno, se crean reglas que cumplen con la confianza mínima requerida.
En la primera fase, se procede de forma constructiva de la siguiente forma (explícitamente se está calculado probabilidad):
Se calcula el soporte de cada ítem y se seleccionan aquellos ítems que cumplen con el soporte mínimo requerido.
Se forman todos las conjuntos (combinaciones) de dos ítems. Sólo se consideran combinaciones de dos ítems que contengan ítems que cumplen el soporte mínimo requerido. Se seleccionan aquellas combinaciones de dos ítems que cumplen con el soporte mínimo requerido.
Se forman todos los conjuntos de tres ítems. No se consideran combinaciones que contengan conjuntos no frecuentes de dos ítems. Es decir, si la combinación {\(x_1\), \(x_4\)} no se frecuente (no cumple con el soporte mínimo requerido), entonces no se consideran combinaciones como {\(x_1\), \(x_3\), \(x_4\)} o {\(x_1\), \(x_2\), \(x_4\)}.
Se continua con las combinaciones de cuatro ítems y se seleccionan aquellas que cumplan con el soporte mínimo requerido. El algoritmo se detiene cuando ya no hay combinaciones de ítems que cumpan con el soporte mínimo.
En la segunda fase, para todas las combinaciones de 2, 3, … ítems, se generan todas las reglas posibles y se evalúa su confianza. Se seleccionan aquellas que cumplen con la confianza mínima requerida. Si la combinación {\(x_1\), \(x_2\)} cumplio con el soporte mínimo, entonces se consideran las reglas {\(x_1\)} \(\to\) {\(x_2\)} y {\(x_2\)} \(\to\) {\(x_1\)}. Nótese que es posible considerar reglas con varios elementos en el consecuente como por ejemplo {\(x_1\)} \(\to\) {\(x_2\), \(x_3\)}.
El lift de una regla mide la importancia de una regla en relación a la tasa típica de compra, dado que se sabe que un ítem o un conjunto de ítems han sido comprados.
Solución usando el lenguaje R¶
A continuación se describen las funcionalidades del paquete arules del lenguaje R para la construcción de reglas de asociación.
Preparación¶
[2]:
## Se instala el paquete
## install.packages("arules")
## Se carga la librería
library(arules)
Formtao del archivo de datos¶
[4]:
##
## arules lee un archivo en formato CSV.
## Se crea un archivo con los datos del
## problema planteado
##
data <- paste(
"x1, x2, x3",
"x1, x3",
"x2, x4",
"x1, x2, x3",
"x1, x2, x5",
"x1, x2, x3, x4",
"x4, x6",
"x1, x2, x4, x6",
"x1, x3, x4",
"x1, x2, x3",
sep="\n")
## Se imprime en pantalla para verificar
cat(data)
## Se escribe el archivo en disco duro
write(data, file = "data/apriori.csv")
x1, x2, x3
x1, x3
x2, x4
x1, x2, x3
x1, x2, x5
x1, x2, x3, x4
x4, x6
x1, x2, x4, x6
x1, x3, x4
x1, x2, x3
Lectura de las transacciones¶
[5]:
##
## Se leen los datos
##
transactions <- read.transactions("data/apriori.csv", sep = ",")
[7]:
##
## Se imprimen los items por transacción
##
inspect(transactions)
items
[1] {x1,x2,x3}
[2] {x1,x3}
[3] {x2,x4}
[4] {x1,x2,x3}
[5] {x1,x2,x5}
[6] {x1,x2,x3,x4}
[7] {x4,x6}
[8] {x1,x2,x4,x6}
[9] {x1,x3,x4}
[10] {x1,x2,x3}
Análisis exploratorio¶
[6]:
##
## Se obtiene la información más relevante de los datos:
##
## * Número de transacciones
## * Número total de ítems
## * Número de transacciones por cantidad de ítems (y cuartiles)
##
summary(transactions)
transactions as itemMatrix in sparse format with
10 rows (elements/itemsets/transactions) and
6 columns (items) and a density of 0.4833333
most frequent items:
x1 x2 x3 x4 x6 (Other)
8 7 6 5 2 1
element (itemset/transaction) length distribution:
sizes
2 3 4
3 5 2
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.00 2.25 3.00 2.90 3.00 4.00
includes extended item information - examples:
labels
1 x1
2 x2
3 x3
[8]:
##
## Se imprime la frequencia de compra, es decir,
## la frecuencia de cada ítem en el total de trasacciones
##
itemFrequency(transactions)
- x1
- 0.8
- x2
- 0.7
- x3
- 0.6
- x4
- 0.5
- x5
- 0.1
- x6
- 0.2
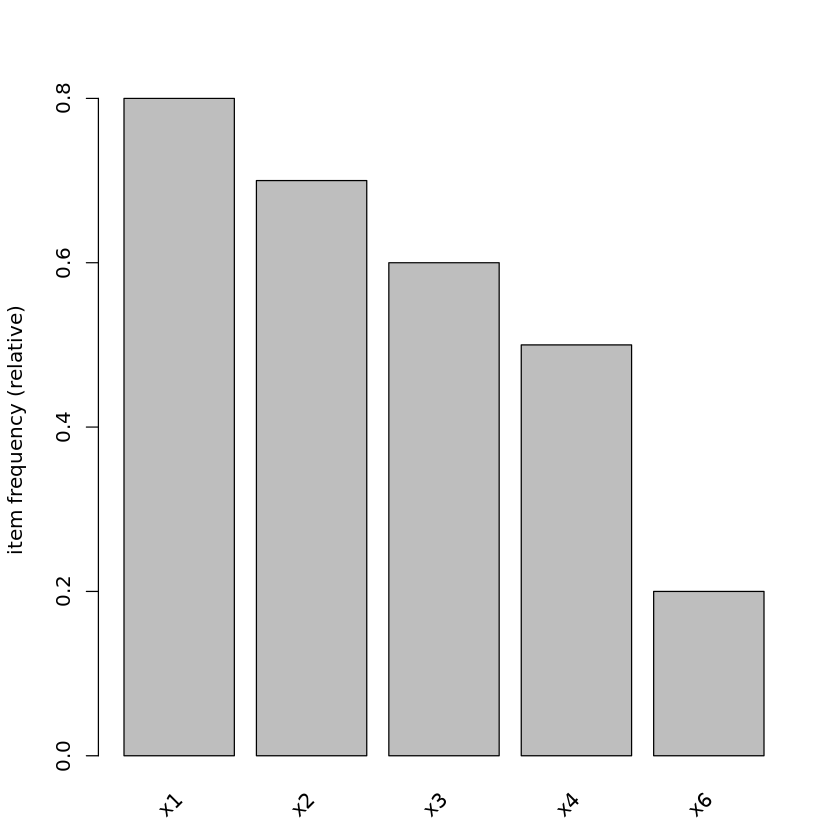
[13]:
##
## Se grafica un histograma que muestra la frecuencia
## con que se compraron ciertos items. El parámetro
## `support` corresponde a la frecuencia mínima que
## deben tener un item para que sea incluído en la gráfica.
## En este caso un item debe aparecer en 0.2 * 10 = 2
## transacciones para ser tenido en cuenta. Nóte que no
## aparece x5.
##
itemFrequencyPlot(transactions, support = 0.2)
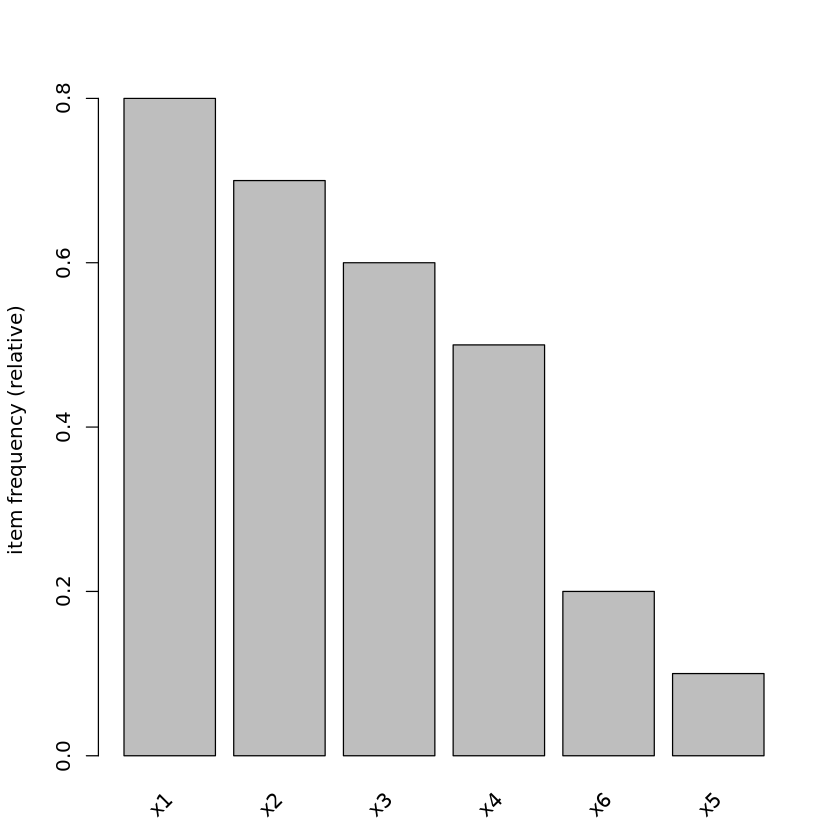
[11]:
##
## Se obtiene la misma gráfica anterior
## pero para los ítems más comprados.
## La gráfica muestra que x1 es el más comprado
## y x5 el menos comprado
##
itemFrequencyPlot(transactions, topN = 6)
Construcción del sistema de reglas de asociación¶
[14]:
##
## La corrida con los parámetros por defecto de la
## función no generan reglas para los datos suministrados.
## El valor por defecto de support es 0.1, es decir,
## un item debe aparecer en un mínimo de 1 transacciones
## para ser considerado.
##
apriori(transactions)
Apriori
Parameter specification:
confidence minval smax arem aval originalSupport maxtime support minlen
0.8 0.1 1 none FALSE TRUE 5 0.1 1
maxlen target ext
10 rules FALSE
Algorithmic control:
filter tree heap memopt load sort verbose
0.1 TRUE TRUE FALSE TRUE 2 TRUE
Absolute minimum support count: 1
set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[6 item(s), 10 transaction(s)] done [0.00s].
sorting and recoding items ... [6 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 done [0.00s].
writing ... [18 rule(s)] done [0.00s].
creating S4 object ... done [0.00s].
set of 18 rules
[16]:
##
## El parámetro confianza representa el porcentaje mínimo
## de veces que una regla debe ser correcta para que
## sea considerada; esto permite eliminar reglas sin
## sentido. El parámetro minlen indica que las reglas
## deben contener al menos 2 items.
##
transactionsrules <- apriori(transactions,
parameter = list(support = 0.006,
confidence = 0.25,
minlen = 2))
Apriori
Parameter specification:
confidence minval smax arem aval originalSupport maxtime support minlen
0.25 0.1 1 none FALSE TRUE 5 0.006 2
maxlen target ext
10 rules FALSE
Algorithmic control:
filter tree heap memopt load sort verbose
0.1 TRUE TRUE FALSE TRUE 2 TRUE
Absolute minimum support count: 0
set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[6 item(s), 10 transaction(s)] done [0.00s].
sorting and recoding items ... [6 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 done [0.00s].
writing ... [48 rule(s)] done [0.00s].
creating S4 object ... done [0.00s].
[18]:
##
## Número de reglas generadas.
## Se generaron 48 reglas
##
transactionsrules
set of 48 rules
[19]:
##
## Se imprime un resumen de las reglas generadas.
##
## * Hay 18 reglas con 2 ítems, 22 reglas con 3 ítems
## y así sucesivamente.
##
## * Luego se imprimen los estadísticos para la cantidad
## de reglas por ítem
##
## * Seguidamente aparece el resumen de las métricas de
## las reglas de asociación
##
summary(transactionsrules)
set of 48 rules
rule length distribution (lhs + rhs):sizes
2 3 4
18 22 8
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 2.000 3.000 2.792 3.000 4.000
summary of quality measures:
support confidence lift count
Min. :0.1000 Min. :0.2500 Min. :0.5000 Min. :1.000
1st Qu.:0.1000 1st Qu.:0.4821 1st Qu.:0.7143 1st Qu.:1.000
Median :0.1000 Median :0.6667 Median :1.0714 Median :1.000
Mean :0.2104 Mean :0.6715 Mean :1.1288 Mean :2.104
3rd Qu.:0.3000 3rd Qu.:1.0000 3rd Qu.:1.2946 3rd Qu.:3.000
Max. :0.6000 Max. :1.0000 Max. :2.5000 Max. :6.000
mining info:
data ntransactions support confidence
transactions 10 0.006 0.25
[23]:
##
## Visualización de todas las reglas.
##
inspect(transactionsrules)
lhs rhs support confidence lift count
[1] {x5} => {x2} 0.1 1.0000000 1.4285714 1
[2] {x5} => {x1} 0.1 1.0000000 1.2500000 1
[3] {x6} => {x4} 0.2 1.0000000 2.0000000 2
[4] {x4} => {x6} 0.2 0.4000000 2.0000000 2
[5] {x6} => {x2} 0.1 0.5000000 0.7142857 1
[6] {x6} => {x1} 0.1 0.5000000 0.6250000 1
[7] {x4} => {x3} 0.2 0.4000000 0.6666667 2
[8] {x3} => {x4} 0.2 0.3333333 0.6666667 2
[9] {x4} => {x2} 0.3 0.6000000 0.8571429 3
[10] {x2} => {x4} 0.3 0.4285714 0.8571429 3
[11] {x4} => {x1} 0.3 0.6000000 0.7500000 3
[12] {x1} => {x4} 0.3 0.3750000 0.7500000 3
[13] {x3} => {x2} 0.4 0.6666667 0.9523810 4
[14] {x2} => {x3} 0.4 0.5714286 0.9523810 4
[15] {x3} => {x1} 0.6 1.0000000 1.2500000 6
[16] {x1} => {x3} 0.6 0.7500000 1.2500000 6
[17] {x2} => {x1} 0.6 0.8571429 1.0714286 6
[18] {x1} => {x2} 0.6 0.7500000 1.0714286 6
[19] {x2,x5} => {x1} 0.1 1.0000000 1.2500000 1
[20] {x1,x5} => {x2} 0.1 1.0000000 1.4285714 1
[21] {x4,x6} => {x2} 0.1 0.5000000 0.7142857 1
[22] {x2,x6} => {x4} 0.1 1.0000000 2.0000000 1
[23] {x2,x4} => {x6} 0.1 0.3333333 1.6666667 1
[24] {x4,x6} => {x1} 0.1 0.5000000 0.6250000 1
[25] {x1,x6} => {x4} 0.1 1.0000000 2.0000000 1
[26] {x1,x4} => {x6} 0.1 0.3333333 1.6666667 1
[27] {x2,x6} => {x1} 0.1 1.0000000 1.2500000 1
[28] {x1,x6} => {x2} 0.1 1.0000000 1.4285714 1
[29] {x3,x4} => {x2} 0.1 0.5000000 0.7142857 1
[30] {x2,x4} => {x3} 0.1 0.3333333 0.5555556 1
[31] {x2,x3} => {x4} 0.1 0.2500000 0.5000000 1
[32] {x3,x4} => {x1} 0.2 1.0000000 1.2500000 2
[33] {x1,x4} => {x3} 0.2 0.6666667 1.1111111 2
[34] {x1,x3} => {x4} 0.2 0.3333333 0.6666667 2
[35] {x2,x4} => {x1} 0.2 0.6666667 0.8333333 2
[36] {x1,x4} => {x2} 0.2 0.6666667 0.9523810 2
[37] {x1,x2} => {x4} 0.2 0.3333333 0.6666667 2
[38] {x2,x3} => {x1} 0.4 1.0000000 1.2500000 4
[39] {x1,x3} => {x2} 0.4 0.6666667 0.9523810 4
[40] {x1,x2} => {x3} 0.4 0.6666667 1.1111111 4
[41] {x2,x4,x6} => {x1} 0.1 1.0000000 1.2500000 1
[42] {x1,x4,x6} => {x2} 0.1 1.0000000 1.4285714 1
[43] {x1,x2,x6} => {x4} 0.1 1.0000000 2.0000000 1
[44] {x1,x2,x4} => {x6} 0.1 0.5000000 2.5000000 1
[45] {x2,x3,x4} => {x1} 0.1 1.0000000 1.2500000 1
[46] {x1,x3,x4} => {x2} 0.1 0.5000000 0.7142857 1
[47] {x1,x2,x4} => {x3} 0.1 0.5000000 0.8333333 1
[48] {x1,x2,x3} => {x4} 0.1 0.2500000 0.5000000 1
[21]:
##
## Se puede inspeccionar un conjunto de reglas en particular
##
inspect(sort(transactionsrules, by = "lift")[1:5])
lhs rhs support confidence lift count
[1] {x1,x2,x4} => {x6} 0.1 0.5 2.5 1
[2] {x6} => {x4} 0.2 1.0 2.0 2
[3] {x4} => {x6} 0.2 0.4 2.0 2
[4] {x2,x6} => {x4} 0.1 1.0 2.0 1
[5] {x1,x6} => {x4} 0.1 1.0 2.0 1
[24]:
##
## Se puede obtener un subconjunto de las reglas que
## cumplen una condición particular
##
berryrules <- subset(transactionsrules, items %in% "x2")
inspect(transactionsrules)
lhs rhs support confidence lift count
[1] {x5} => {x2} 0.1 1.0000000 1.4285714 1
[2] {x5} => {x1} 0.1 1.0000000 1.2500000 1
[3] {x6} => {x4} 0.2 1.0000000 2.0000000 2
[4] {x4} => {x6} 0.2 0.4000000 2.0000000 2
[5] {x6} => {x2} 0.1 0.5000000 0.7142857 1
[6] {x6} => {x1} 0.1 0.5000000 0.6250000 1
[7] {x4} => {x3} 0.2 0.4000000 0.6666667 2
[8] {x3} => {x4} 0.2 0.3333333 0.6666667 2
[9] {x4} => {x2} 0.3 0.6000000 0.8571429 3
[10] {x2} => {x4} 0.3 0.4285714 0.8571429 3
[11] {x4} => {x1} 0.3 0.6000000 0.7500000 3
[12] {x1} => {x4} 0.3 0.3750000 0.7500000 3
[13] {x3} => {x2} 0.4 0.6666667 0.9523810 4
[14] {x2} => {x3} 0.4 0.5714286 0.9523810 4
[15] {x3} => {x1} 0.6 1.0000000 1.2500000 6
[16] {x1} => {x3} 0.6 0.7500000 1.2500000 6
[17] {x2} => {x1} 0.6 0.8571429 1.0714286 6
[18] {x1} => {x2} 0.6 0.7500000 1.0714286 6
[19] {x2,x5} => {x1} 0.1 1.0000000 1.2500000 1
[20] {x1,x5} => {x2} 0.1 1.0000000 1.4285714 1
[21] {x4,x6} => {x2} 0.1 0.5000000 0.7142857 1
[22] {x2,x6} => {x4} 0.1 1.0000000 2.0000000 1
[23] {x2,x4} => {x6} 0.1 0.3333333 1.6666667 1
[24] {x4,x6} => {x1} 0.1 0.5000000 0.6250000 1
[25] {x1,x6} => {x4} 0.1 1.0000000 2.0000000 1
[26] {x1,x4} => {x6} 0.1 0.3333333 1.6666667 1
[27] {x2,x6} => {x1} 0.1 1.0000000 1.2500000 1
[28] {x1,x6} => {x2} 0.1 1.0000000 1.4285714 1
[29] {x3,x4} => {x2} 0.1 0.5000000 0.7142857 1
[30] {x2,x4} => {x3} 0.1 0.3333333 0.5555556 1
[31] {x2,x3} => {x4} 0.1 0.2500000 0.5000000 1
[32] {x3,x4} => {x1} 0.2 1.0000000 1.2500000 2
[33] {x1,x4} => {x3} 0.2 0.6666667 1.1111111 2
[34] {x1,x3} => {x4} 0.2 0.3333333 0.6666667 2
[35] {x2,x4} => {x1} 0.2 0.6666667 0.8333333 2
[36] {x1,x4} => {x2} 0.2 0.6666667 0.9523810 2
[37] {x1,x2} => {x4} 0.2 0.3333333 0.6666667 2
[38] {x2,x3} => {x1} 0.4 1.0000000 1.2500000 4
[39] {x1,x3} => {x2} 0.4 0.6666667 0.9523810 4
[40] {x1,x2} => {x3} 0.4 0.6666667 1.1111111 4
[41] {x2,x4,x6} => {x1} 0.1 1.0000000 1.2500000 1
[42] {x1,x4,x6} => {x2} 0.1 1.0000000 1.4285714 1
[43] {x1,x2,x6} => {x4} 0.1 1.0000000 2.0000000 1
[44] {x1,x2,x4} => {x6} 0.1 0.5000000 2.5000000 1
[45] {x2,x3,x4} => {x1} 0.1 1.0000000 1.2500000 1
[46] {x1,x3,x4} => {x2} 0.1 0.5000000 0.7142857 1
[47] {x1,x2,x4} => {x3} 0.1 0.5000000 0.8333333 1
[48] {x1,x2,x3} => {x4} 0.1 0.2500000 0.5000000 1