Tangentes, derivadas y gradiente#
Ultima modificación: Feb 01, 2024 | YouTube
Pendiente entre dos puntos de una función#
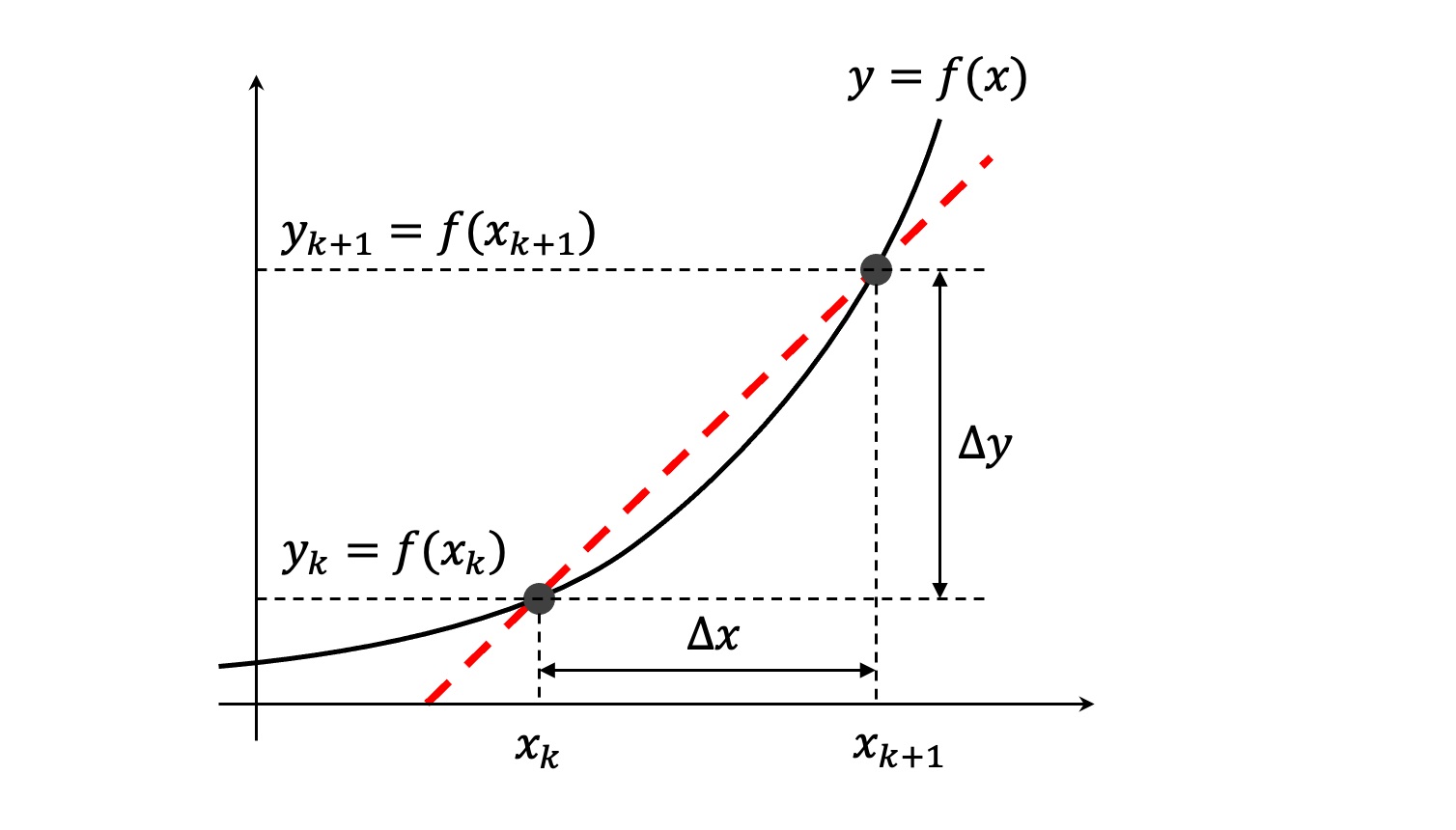
La pendiente entre los puntos x_k y x_{k+1} es:
\begin{split} m & = \frac{y_{k+1} - y_k}{x_{k+1} - x_k} \\ \\ & = \frac{f(x_{k+1}) - f(x_k)}{x_{k+1} - x_k} \end{split}
Si se tiene en cuenta que \Delta x = x_{k+1} - x_k y x_{k+1} = x_k + \Delta x, entonces:
\begin{split} m & = \frac{f(x_{k+1}) - f(x_k)}{x_{k+1} - x_k} \\ \\ & = \frac{f(x_k + \Delta x) - f(x_k)}{\Delta x} \\ \end{split}
Concepto de derivada#
Se obtiene al hacer \Delta x tienda a cero. De esta forma, la línea roja se hace tangente a la función f(x) en el punto x_k.
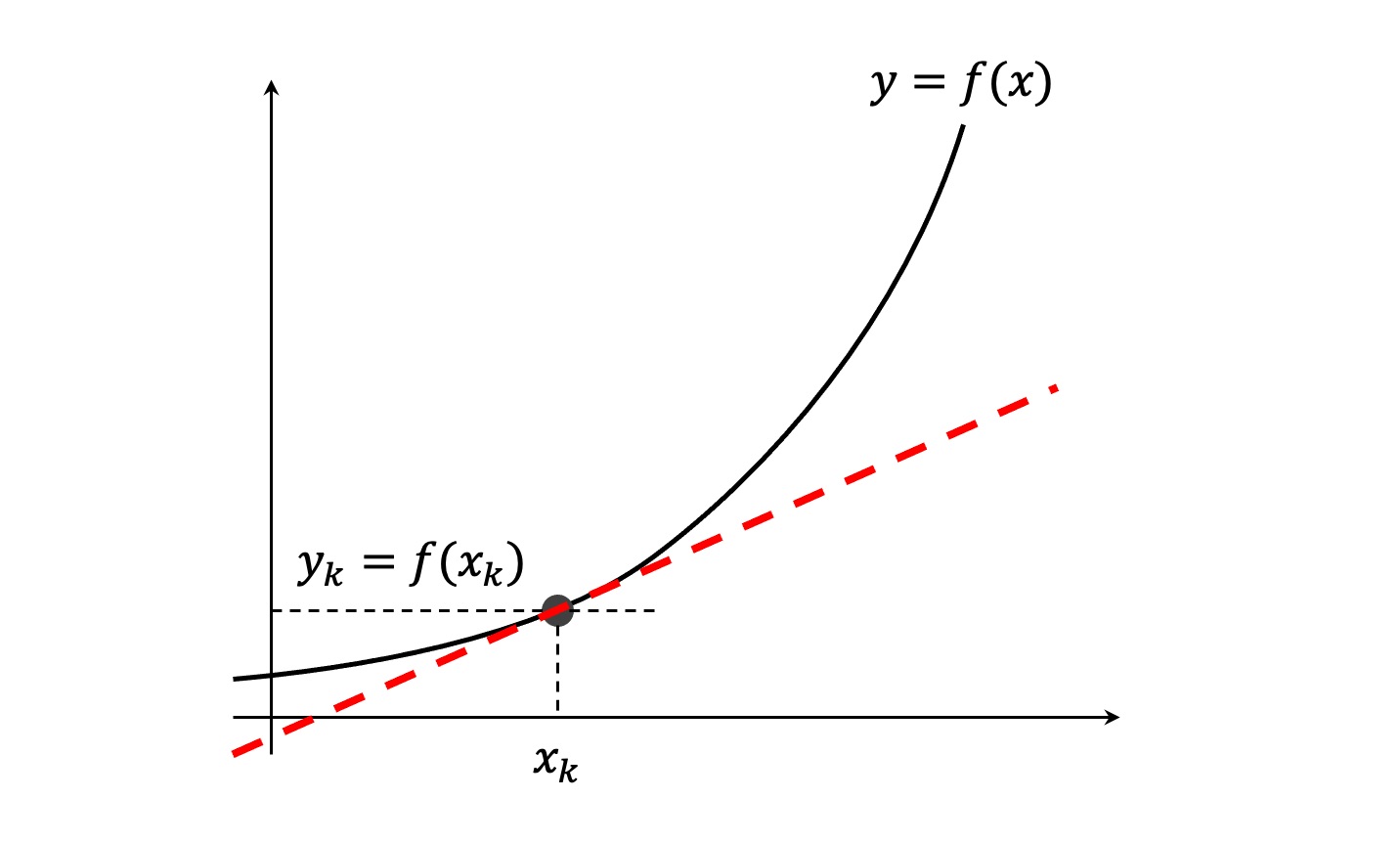
En términos matemáticos:
\frac{d}{dx} f(x_k) = \lim_{\Delta x \to 0} \frac{f(x_k + \Delta x) - f(x_k)}{\Delta x}
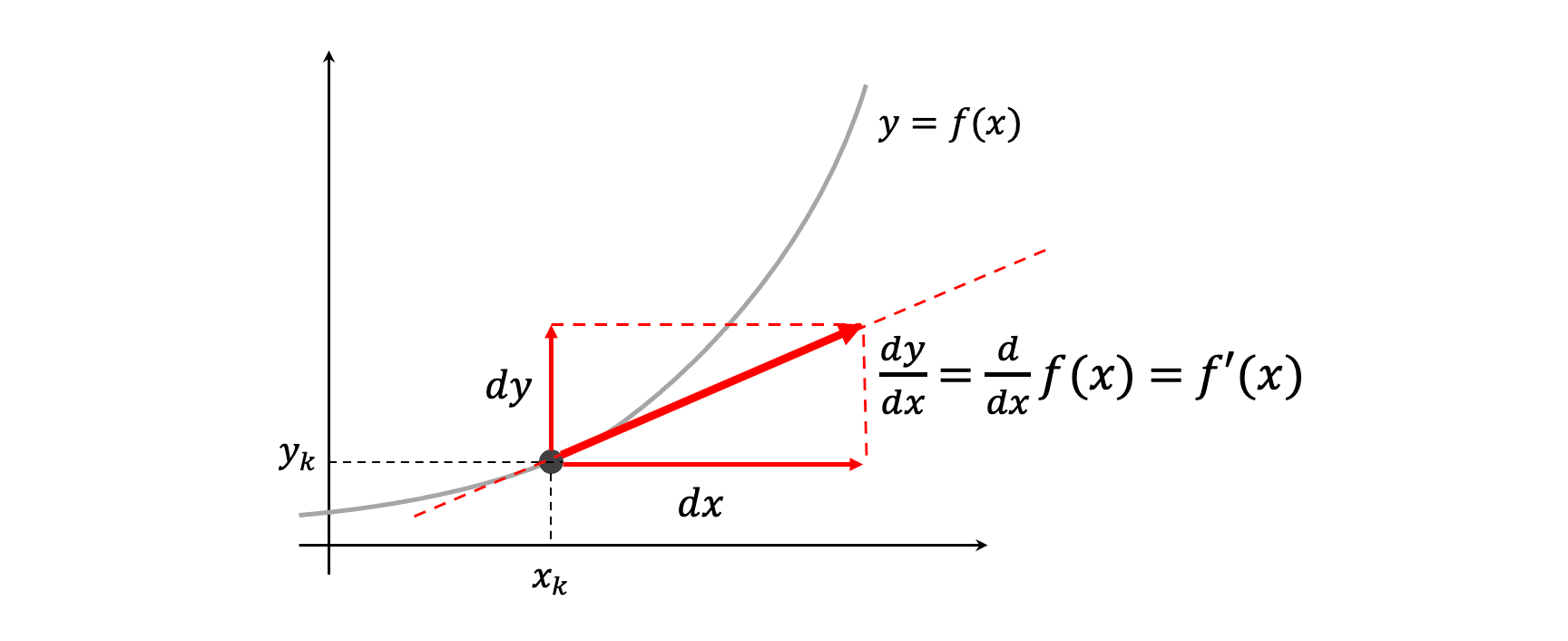
y por tanto, la derivada es la pendiente de la recta tangente a f(x) en el punto x.
Notación#
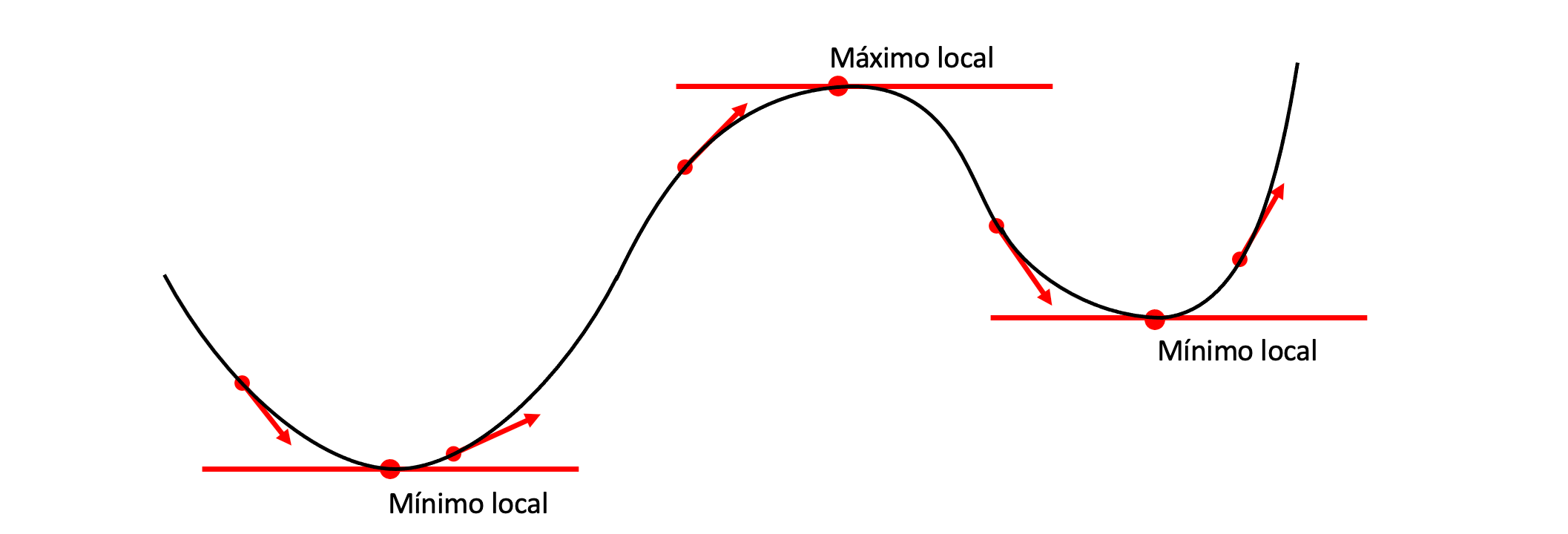
Signo de la derivada para distintas formas de f(x)#
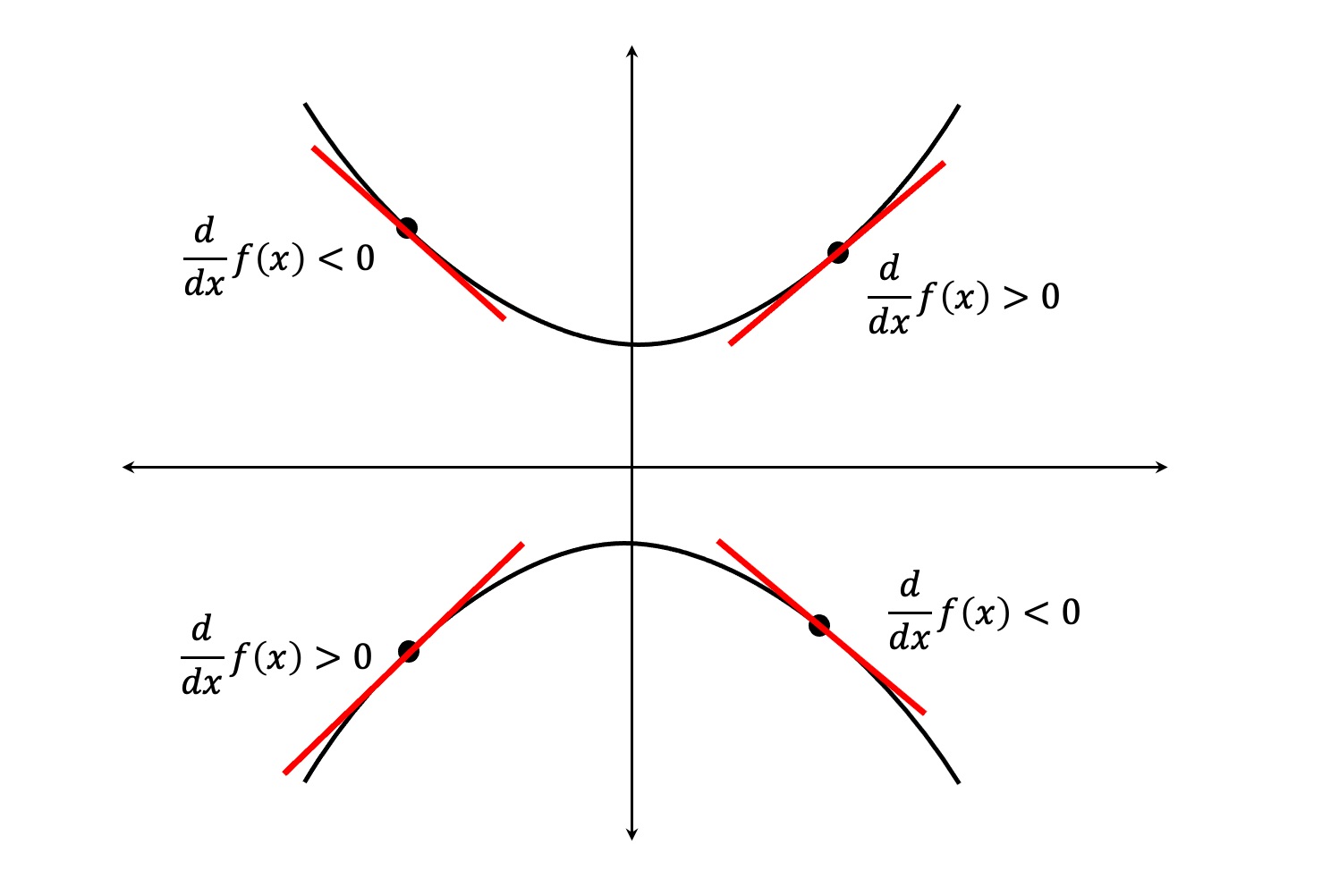
En la siguiente figura se consideran varias formas de f(x) y se desea determinar el signo de la derivada en un punto x.
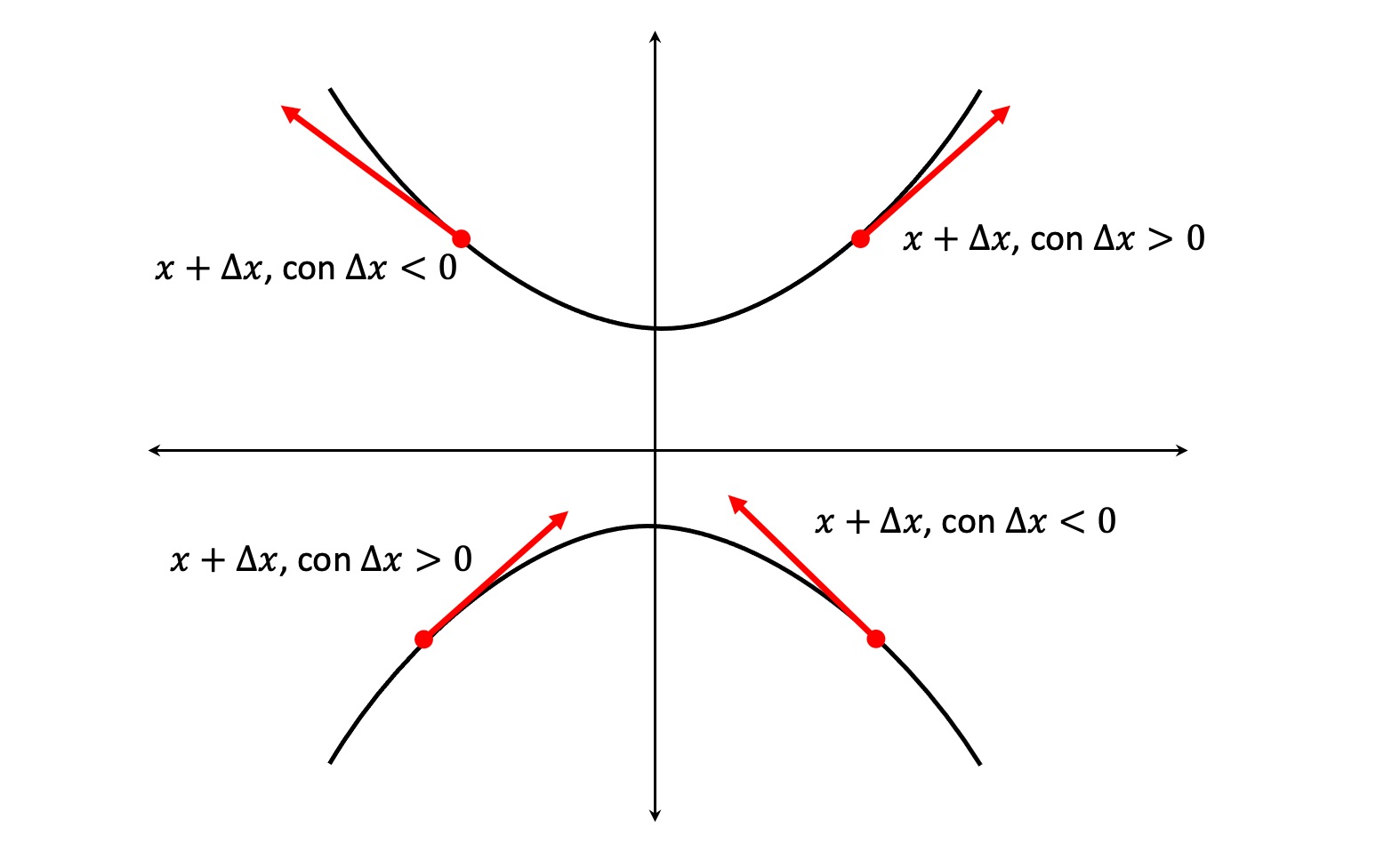
Dirección de x + \Delta x si \Delta x tiene el mismo signo de la derivada#
Si a x se le suma un valor \Delta x que tiene el mismo signo de la derivada, x se moverá en la dirección del crecimiento de la función. Este es el gradiente de la función.
Derivada y puntos de máxima y mínima#