Algunas derivadas comunes#
Ultima modificación: Feb 01, 2024 | YouTube
Derivada de una constante#
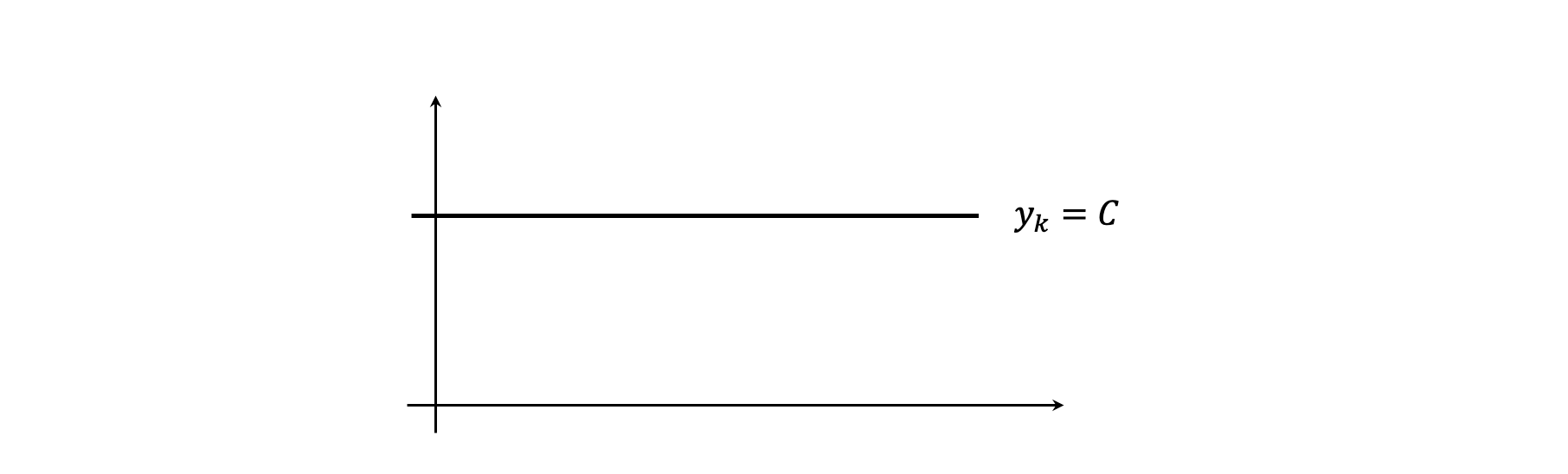
La pendiente entre los puntos x_k y x_{k+1} es:
\begin{split} m & = \frac{y_{k+1} - y_k}{x_{k+1} - x_k} \\ \\ & = \frac{f(x_{k+1}) - f(x_k)}{x_{k+1} - x_k} \\ \\ & = \frac{C - C}{x_{k+1} - x_k} \\ \\ & = \frac{0}{x_{k+1} - x_k} \\ \\ & = 0 \end{split}
Derivada de una línea#
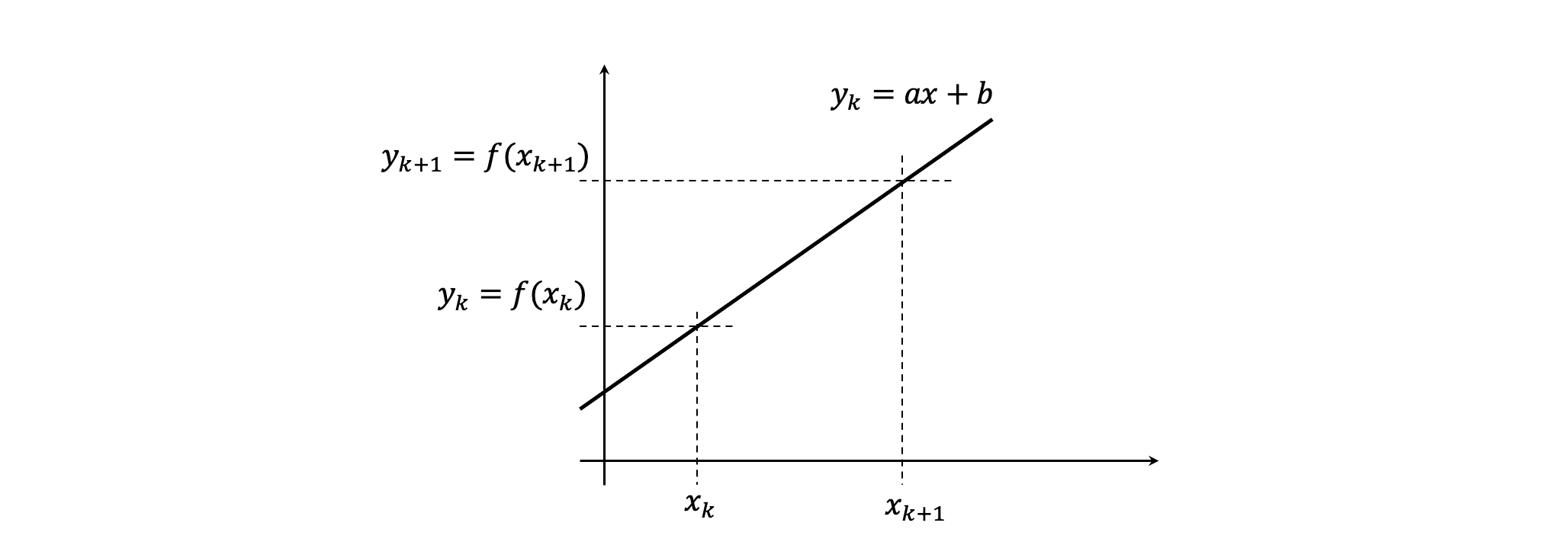
La pendiente entre los puntos x_k y x_{k+1} es:
\begin{split} m & = \frac{y_{k+1} - y_k}{x_{k+1} - x_k} \\ \\ & = \frac{f(x_{k+1}) - f(x_k)}{x_{k+1} - x_k} \\ \\ & = \frac{(a \cdot x_{k+1} + b) - (a \cdot x_{k} + b)}{x_{k+1} - x_k} \\ \\ & = \frac{a \cdot x_{k+1} + b - a \cdot x_{k} - b}{x_{k+1} - x_k} \\ \\ & = \frac{a \cdot x_{k+1} - a \cdot x_{k} }{x_{k+1} - x_k} \\ \\ & = a \cdot \frac{x_{k+1} - x_{k} }{x_{k+1} - x_k} \\ \\ & = a \end{split}
Derivada de una cuadrática#
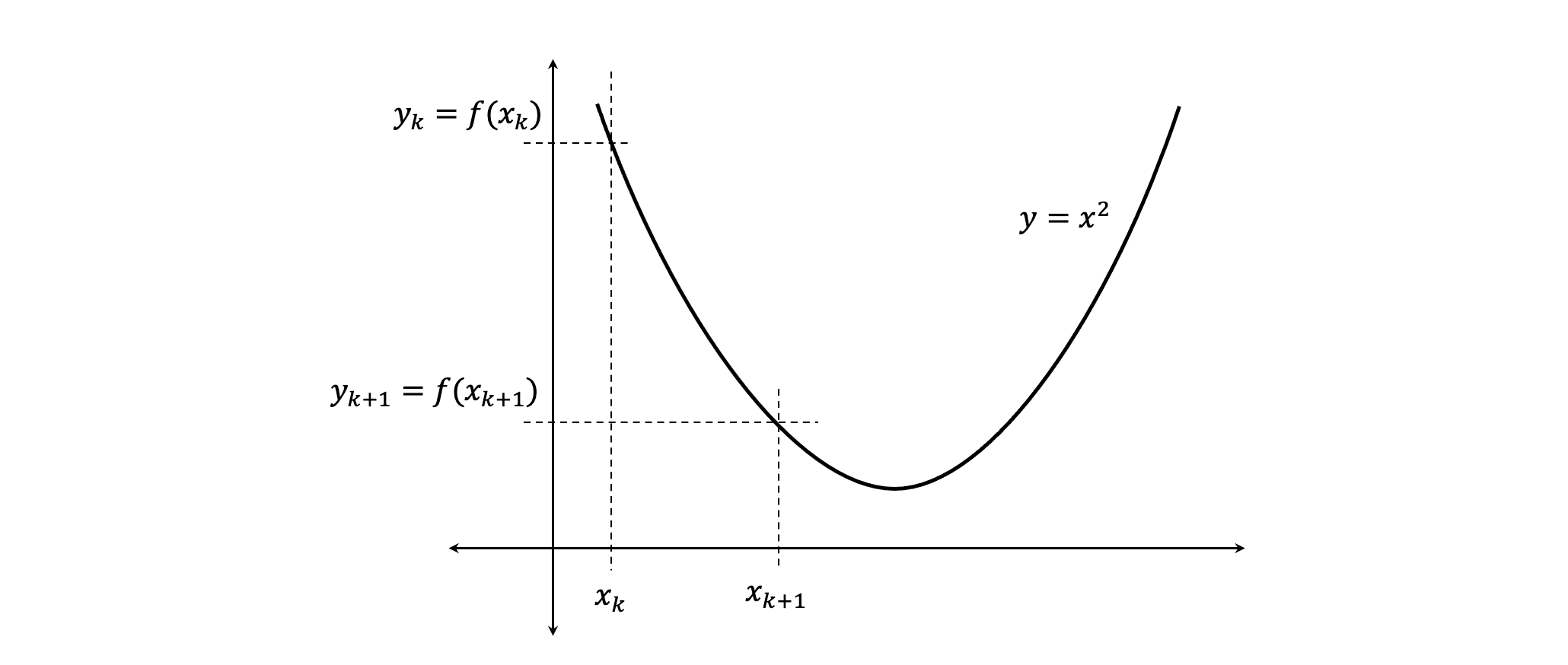
La pendiente entre los puntos x_k y x_{k+1} es:
\begin{split} m & = \frac{y_{k+1} - y_k}{x_{k+1} - x_k} \\ \\ & = \frac{f(x_{k+1}) - f(x_k)}{x_{k+1} - x_k} \\ \\ & = \frac{(x_{k+1})^2 - (x_k)^2}{x_{k+1} - x_k} \\ \\ & = \frac{(x_k + \Delta x)^2 - (x_k)^2}{\Delta x} \\ \\ & = \frac{(x_k)^2 + 2 \cdot x_k \cdot \Delta x + (\Delta x)^2 - (x_k)^2}{\Delta x} \\ \\ & = \frac{ 2 \cdot x_k \cdot \Delta x + (\Delta x)^2 }{\Delta x} \\ \\ & = 2 \cdot x_k + \Delta x \end{split}
Tomando el límite:
\frac{d}{dx} f(x_k) = \lim_{\Delta x \to 0} 2 \cdot x_k + \Delta x = 2x_k
Derivada de x^n#
\frac{d}{dx} f(x) = \frac{d}{dx} x^n = n \cdot x^{n-1}
Derivada de 1/x#
\begin{split} \frac{d}{dx} f(x) & = \frac{d}{dx} \frac{1}{x} \\ \\ & = \frac{d}{dx} x^{-1} \\ \\ & = (-1) \cdot x^{-1 - 1} \\ \\ & = - x^{-2} \\ \\ \end{split}
Derivada de la inversa de una función#
Función:
y = f(x)
Función inversa:
g(y) = x
Por definición:
g(f(x)) = x
Derivada:
g'(y) = \frac{1}{f'(x)}
Derivada de funciones trigonométricas#
f(x) = \sin(x), f'(x) = \cos(x)
f(x) = \cos(x), f'(x) = - \sin(x)
Derivada de e^x y \log (x)#
\frac{d}{dx} \exp (x) = \exp(x)
\frac{d}{dx} \log(x) = \frac{1}{x}