Aprendizaje online y gradiente descendente estocástico

• Ultima modificación: Feb 01, 2024 | YouTube

Definición del problema de estimación de parámetros

Se desean encontra los parámetros w_0 y w_1 del siguiente modelo de regresión entre las variables x y y:

y_i = w_1 x_i + w_0 + e_i

a partir de un conjunto de observaciones \{d_i, x_i\}, donde d_i es el valor real (observado), y_i es su aproximación usando el modelo de regresión descrito, y e_i es el error.

Función de pérdida

La sumatoria de errores al cuadrado es definido como:

\text{SSE}(w_0, w_1) = \sum_i (d_i - y_i)^2

Si se tiene en cuenta que el error instantáneo se define como:

e_i = d_i - y_i

la ecuación anterior se puede reescribir como:

\begin{split} \text{SSE}(w_0, w_1) & = \sum_i (d_i - y_i)^2 \\ & = \sum_i e_i^2 \end{split}

Aprendizaje Batch

De acuerdo con el método del gradiente:

\begin{split} \mathbf{w}_k & = \mathbf{w}_{k-1} - \mu \frac{\partial}{\partial \mathbf{w}} \text{SSE}(\mathbf{w}_{k-1}) \\ & = \mathbf{w}_{k-1} - \mu \frac{\partial}{\partial \mathbf{w}} \left( \sum_i e_i^2 \right) \end{split}

donde \mathbf{w} = [w_0, w_1].

La ecuación anterior se puede reescribir como:

\mathbf{w}_k = \mathbf{w}_{k-1} - \mu \sum_i \left( \frac{\partial}{\partial \mathbf{w}} e_i^2 \right)

Aprendizaje online

El aprendizaje online se obtiene al hacer una corrección de los parámetros de forma secuencial para cada punto i. El nombre del método se deriva del hecho de que los puntos

(x_i, y_i)

pueden presentarse al algoritmo como un stream de datos.

Es decir, la ecuación de corrección cambia a:

\mathbf{w}_k = \mathbf{w}_{k-1} - \mu \left( \frac{\partial}{\partial \mathbf{w}} e_i^2 \right)

El proceso es el siguiente:

• Se computa el gradiente instantáneo para el punto i.

• Se realiza la corrección del vector de parámetros \mathbf{w}_k con el gradiente para el punto i.

• Se pasa al siguiente punto (i = i + 1) y se rotorna al primer paso.

Derivadas

Las derivadas del error instantáneo son:

\begin{split} \frac{\partial}{\partial w_0} e^2_i & = -2 e_i \\ \end{split}

\begin{split} \frac{\partial}{\partial w_1} e^2_i & = -2 e_i x_i \\ \end{split}

Ejemplo numérico

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm

#
# Datos del problema
#
x_sample = [
    0.6231,
    0.7460,
    0.1087,
    0.3654,
    0.3065,
    0.6886,
    0.4966,
    0.2618,
    0.7607,
    0.4424,
    0.7731,
]

y_sample = [
    1.6266,
    1.8508,
    0.9519,
    1.2828,
    1.2283,
    1.8722,
    1.4657,
    1.1097,
    1.7826,
    1.4267,
    1.8248,
]

#
# Sumatoria del error cuadrático o pérdida cuadrática
#
def sse(w0, w1):
    y_forecasts = [w0 + w1 * x_value for x_value in x_sample]
    errors = [y_true - y_forecast for y_true, y_forecast in zip(y_sample, y_forecasts)]
    squared_errors = [error ** 2 for error in errors]
    return sum(squared_errors)

def plot_contour():

    W0 = np.linspace(0.0, 0.8, 50)
    W1 = np.linspace(2.4, 3.2, 50)
    W0, W1 = np.meshgrid(W0, W1)
    F = sse(W0, W1)

    levels = [0, 0.2, 0.5, 0.75, 1, 2, 3, 5, 10, 20, 40, 60]

    fig, ax = plt.subplots(figsize=(3.5, 3.5))

    ax.set_aspect("equal", "box")
    ax.contourf(W0, W1, F, cmap=cm.Greys, levels=levels, alpha=0.8)
    ax.contour(W0, W1, F, colors="gray", levels=levels)
    ax.grid()
    ax.set_xlabel("w0")
    ax.set_ylabel("w1")

def gradient(w0, w1, x_value, y_value):

    error = y_value - w0 - w1 * x_value
    gradient_w0 = -2 * error
    gradient_w1 = -2 * error * x_value

    return gradient_w0, gradient_w1

Ecuación de mejora

\mathbf{w}_k = \mathbf{w}_{k-1} - \mu \left( \frac{\partial}{\partial \mathbf{w}} e_i^2 \right)

def improve(w0, w1, mu, x_value, y_value):

    gradient_w0, gradient_w1 = gradient(w0, w1, x_value, y_value)
    w0 = w0 - mu * gradient_w0
    w1 = w1 - mu * gradient_w1

    return w0, w1

Proceso iterativo del aprendizaje online

#
# Punto de inicio
#
w0 = 0.5
w1 = 3.0

history = {
    "w0": [w0],
    "w1": [w1],
    "sse": [sse(w0, w1)],
}

mu = 0.03

for epoch in range(10):

    for x_value, y_value in zip(x_sample, y_sample):

        w0, w1 = improve(w0, w1, mu, x_value, y_value)

        history["w0"].append(w0)
        history["w1"].append(w1)
        history["sse"].append(sse(w0, w1))

print(" w0 = {:6.4f}\n w1 = {:6.4f}\nSSE = {:6.4f}\n".format(w0, w1, sse(w0, w1)))

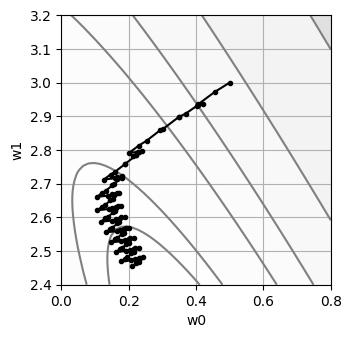
plot_contour()
plt.plot(history["w0"], history["w1"], marker=".", color="black")
plt.show()

 w0 = 0.2106
 w1 = 2.4542
SSE = 0.6276

plt.figure(figsize=(10, 3.5))
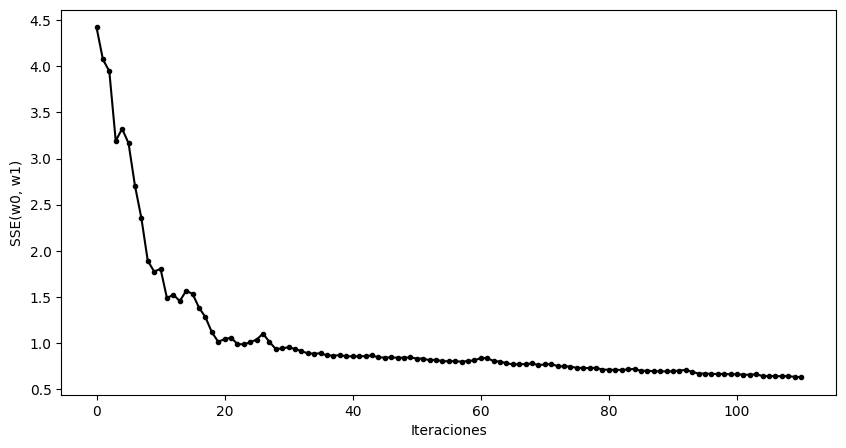
plt.plot(history["sse"], ".-k")
plt.xlabel("Iteraciones")
plt.ylabel("SSE(w0, w1)")
plt.show()

Gradiente descendente estocástico

El método del gradiente descendente estocástico es el método de aprendizaje online en el que los patrones se recorren de forma aleatoria.

#
# Punto de inicio
#
w0 = 0.5
w1 = 3.0

history = {
    "w0": [w0],
    "w1": [w1],
    "sse": [sse(w0, w1)],
}

mu = 0.03

n_samples = len(x_sample)

for epoch in range(10):

    for n in np.random.choice(n_samples, n_samples, replace=False):

        w0, w1 = improve(w0, w1, mu, x_sample[n], y_sample[n])

        history["w0"].append(w0)
        history["w1"].append(w1)
        history["sse"].append(sse(w0, w1))

print(" w0 = {:6.4f}\n w1 = {:6.4f}\nSSE = {:6.4f}\n".format(w0, w1, sse(w0, w1)))

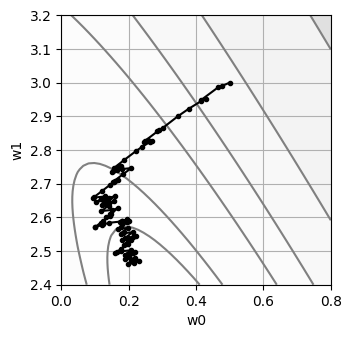
plot_contour()
plt.plot(history["w0"], history["w1"], marker=".", color="black");

 w0 = 0.2306
 w1 = 2.4693
SSE = 0.6293

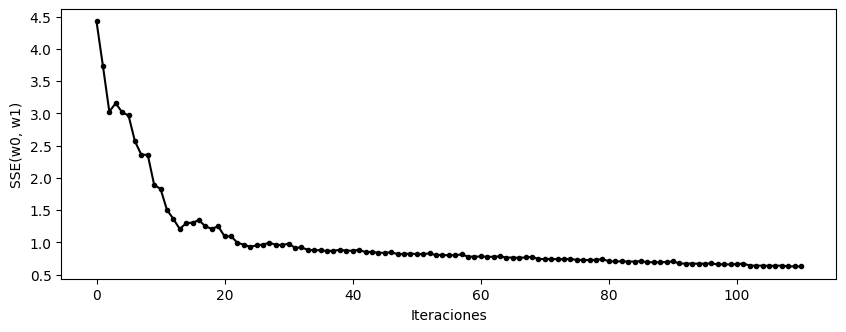
plt.figure(figsize=(10, 5))
plt.plot(history["sse"], ".-k")
plt.xlabel("Iteraciones")
plt.ylabel("SSE(w0, w1)")
plt.show()