Aprendizaje batch#
Ultima modificación: Feb 01, 2024 | YouTube
[1]:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
Definición del problema de regresión univariada#
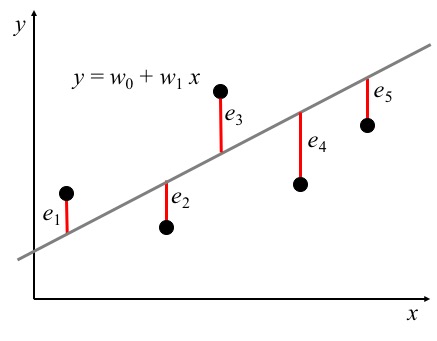
Se desean encontra los parámetros w_0 y w_1 del siguiente modelo de regresión entre las variables x y y:
y_i = w_1 x_i + w_0 + e_i
a partir de un conjunto de observaciones \{d_i, x_i\}, donde d_i es el valor real (observado), y_i es su aproximación usando el modelo de regresión descrito, y e_i es el error.
[2]:
#
# Datos del problema
#
x_sample = np.array(
[
0.1087,
0.2698,
0.3765,
0.2146,
0.9155,
0.0246,
0.0221,
0.8632,
0.6460,
0.2092,
0.8567,
0.1591,
0.9647,
0.6231,
0.7460,
0.3654,
0.3065,
0.6886,
0.4966,
0.2008,
0.2618,
0.7607,
0.1563,
0.4424,
0.7731,
]
)
y_sample = np.array(
[
0.9519,
1.1237,
1.2360,
1.0526,
2.0743,
0.7906,
0.7603,
2.0533,
1.6887,
1.0563,
2.0991,
0.8953,
2.1917,
1.6266,
1.8508,
1.2828,
1.2283,
1.8722,
1.4657,
1.0418,
1.1097,
1.7826,
0.9711,
1.4267,
1.8248,
]
)
En otras palabras, se desean encontrar los parámetros w_0 y w_1 de la recta
y_i = w_0 + w_1 * x_i
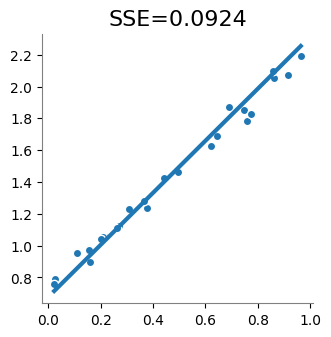
que minimicen la suma de los errores cuadráticos entre el valor real d_i y el valor pronósticado y_i para cada valor posible de la variable x_i, tal como se ilustra en la gráfica de abajo. El error e_i se define como d_i - y_i.
Función de pérdida#
Se desea encontrar la combinación de parámetros w_0 y w_1 que minimice:
\begin{split} \text{SSE} & = \sum_i e_i^2 \\ & = \sum_i (d_i - y_i)^2 \\ & = \sum_i (d_i - w_0 - w_1 x_i)^2 \end{split}
Note que en la ecuación anterior, los valores de x_i y d_i son constantes que corresponden a la tabla de datos presentada en la formulación del problema, mientras que las variables son w_0 y w_1, de tal forma que:
\text{SSE}(w_0, w_1) = \sum_i (d_i - w_0 - w_1 x_i)^2
[3]:
#
# Sumatoria del error cuadrático o pérdida cuadrática
#
def sse(w0, w1):
y_forecasts = [w0 + w1 * x_value for x_value in x_sample]
errors = [y_true - y_forecast for y_true, y_forecast in zip(y_sample, y_forecasts)]
squared_errors = [error**2 for error in errors]
return sum(squared_errors)
Pronóstico del modelo para valores arbitrarios#
[4]:
def plot_forecast(w0, w1):
z_sample = np.linspace(min(x_sample), max(x_sample))
y_forecasts = w0 + w1 * z_sample
plt.scatter(x_sample, y_sample, color="tab:blue", edgecolors="white")
plt.plot(z_sample, y_forecasts, "-", color="tab:blue", linewidth=3)
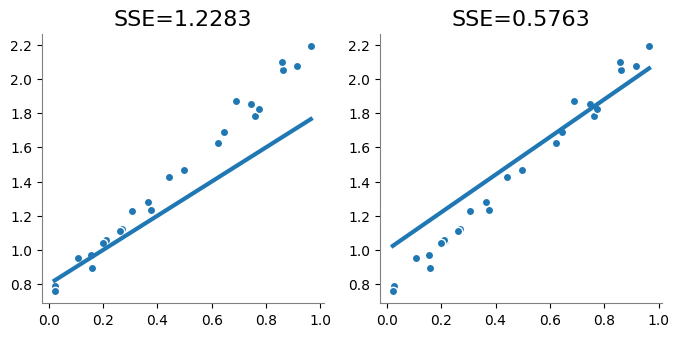
plt.title(
"SSE=" + str(round(sse(w0, w1), 4)),
fontsize=16,
)
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.figure(figsize=(8, 3.5))
plt.subplot(1, 2, 1)
plot_forecast(w0=0.8, w1=1)
plt.subplot(1, 2, 2)
plot_forecast(w0=1.0, w1=1.1)
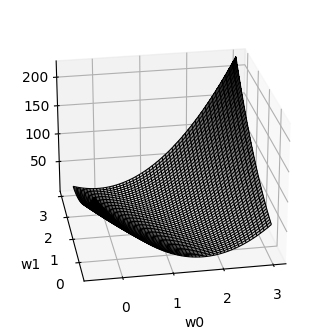
Forma de la superficie de la función de pérdida#
Ya que la función SSE() depende únicamente de los valores de w_0 y w_1, es posible graficar su forma.
[5]:
def plot_surface():
W0 = np.linspace(-0.5, 3.0, 50)
W1 = np.linspace(-0.5, 3.0, 50)
W0, W1 = np.meshgrid(W0, W1)
F = sse(W0, W1)
#
# Superficie de error
#
ax = plt.figure(figsize=(4, 4)).add_subplot(projection="3d", azim=-100, elev=25)
ax.plot_surface(W0, W1, F, cmap=cm.binary, linewidth=1, antialiased=False)
ax.plot_wireframe(W0, W1, F, color="black", linewidth=0.8, alpha=1.0)
plt.xlabel("w0")
plt.ylabel("w1")
plot_surface()
plt.show()
Contorno de la función de pérdida#
[6]:
def plot_contour():
W0 = np.linspace(-0.5, 1.5, 100)
W1 = np.linspace(1.0, 3.0, 100)
W0, W1 = np.meshgrid(W0, W1)
F = sse(W0, W1)
levels = [0, 0.2, 0.5, 0.75, 1, 2, 3, 5, 10, 20, 30, 40, 50, 60]
_, ax = plt.subplots(figsize=(3.5, 3.5))
ax.set_aspect("equal", "box")
ax.contourf(W0, W1, F, cmap=cm.Greys, levels=levels, alpha=0.8)
ax.contour(W0, W1, F, colors="gray", levels=levels)
plt.plot(
[0.731],
[1.498],
"o",
color="black",
fillstyle="none",
markersize=11,
markeredgewidth=2,
)
plt.plot([0.731], [1.498], ".", color="black")
ax.set_xlabel("w0")
ax.set_ylabel("w1")
ax.grid()
plot_contour()
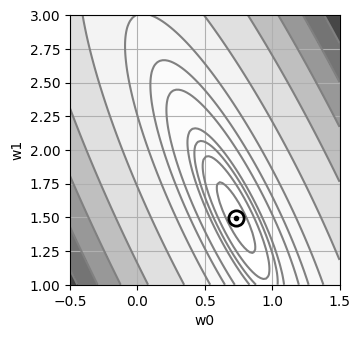
En términos de optimización, se desea encontrar las coordenadas (w_0, w_1) del punto más bajo (error mínimo) de la superficie de error.
La función de error es una cuadrática (forma de tazón) con un único punto de mínima global.
Gradiente algebraico de la función de pérdida#
La función de pérdida está definida como:
\text{SSE}(w_0, w_1) = \sum_i (d_i - w_0 - w_1 x_i)^2
La derivada respecto a w_0 es:
\begin{split} \frac{\partial}{\partial w_0} \text{SSE}(w_0, w_1) & = \frac{\partial}{\partial w_0} \sum_i (d_i - y_i)^2 \\ & = \frac{\partial}{\partial w_0} \sum_i (d_i - w_0 - w_1 x_i)^2 \\ & = \sum_i \frac{\partial}{\partial w_0} (d_i - w_0 - w_1 x_i)^2 \\ & = \sum_i 2 \times (d_i - w_0 - w_1 x_i) \times \frac{\partial}{\partial w_0} (d_i - w_0 - w_1 x_i) \\ & = \sum_i 2 \times e_i \times (-1) \\ & = -2 \sum_i e_i \\ \end{split}
La derivada respecto a w_1 es:
\begin{split} \frac{\partial}{\partial w_1} \text{SSE}(w_0, w_1) & = \frac{\partial}{\partial w_1} \sum_i (d_i - y_i)^2 \\ & = \frac{\partial}{\partial w_1} \sum_i (d_i - w_0 - w_1 x_i)^2 \\ & = \sum_i \frac{\partial}{\partial w_1} (d_i - w_0 - w_1 x_i)^2 \\ & = \sum_i 2 * (d_i - w_0 - w_1 x_i) \times \frac{\partial}{\partial w_1} (d_i - w_0 - w_1 x_i) \\ & = \sum_i 2 * e_i \times (-x_i) \\ & = -2 \sum_i e_i x_i \\ \end{split}
Si los parámetros w_0 y w_1 se agrupan en el vector de parámetros \mathbf{w}=[w_0, w_1]', entonces:
\frac{\partial}{\partial \mathbf{w}} \text{SSE}(\mathbf{w}) = \left[ \begin{array}{c} -2 \sum_i e_i \\ -2 \sum_i e_i x_i \end{array} \right]
Codificación del gradiente#
\mathbf{w}_k = \mathbf{w}_{k-1} - \mu \frac{\partial}{\partial \mathbf{w}} \text{SSE}(\mathbf{w}_{k-1})
De esta forma, la función que computa el gradiente se implementa como:
[7]:
def gradient(w0, w1):
y_forecasts = [w0 + w1 * x_value for x_value in x_sample]
errors = [y_true - y_forecast for y_true, y_forecast in zip(y_sample, y_forecasts)]
gradient_w0 = -2 * sum(errors)
gradient_w1 = -2 * sum(
[error * x_value for error, x_value in zip(errors, x_sample)]
)
return gradient_w0, gradient_w1
Ecuación de mejora#
A partir de las definiciones y cómputos anteriores, es posible implementar el proceso iterativo de mejora de los pesos usando la ecuación:
\mathbf{w}_k = \mathbf{w}_{k-1} - \mu \frac{\partial}{\partial \mathbf{w}} \text{SSE}(\mathbf{w}_{k-1})
[8]:
def improve(w0, w1, mu):
gradient_w0, gradient_w1 = gradient(w0, w1)
w0 = w0 - mu * gradient_w0
w1 = w1 - mu * gradient_w1
return w0, w1
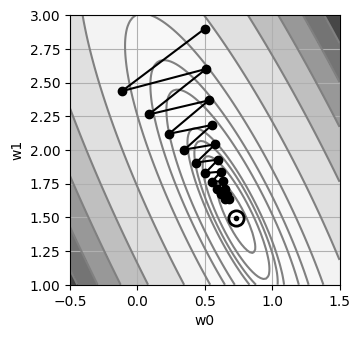
Proceso iterativo#
Para realizar la optimización numérica, se parte de unos pesos iniciales aleatorios.
[9]:
#
# Punto de inicio
#
w0 = 0.5
w1 = 2.9
history = {
"w0": [w0],
"w1": [w1],
"sse": [sse(w0, w1)],
}
mu = 0.03
for epoch in range(20):
w0, w1 = improve(w0, w1, mu)
history["w0"].append(w0)
history["w1"].append(w1)
history["sse"].append(sse(w0, w1))
print(" w0 = {:6.4f}\n w1 = {:6.4f}\nSSE = {:6.4f}".format(w0, w1, sse(w0, w1)))
plot_contour()
plt.plot(history["w0"], history["w1"], marker="o", color="black")
plt.show()
w0 = 0.6786
w1 = 1.6341
SSE = 0.0924
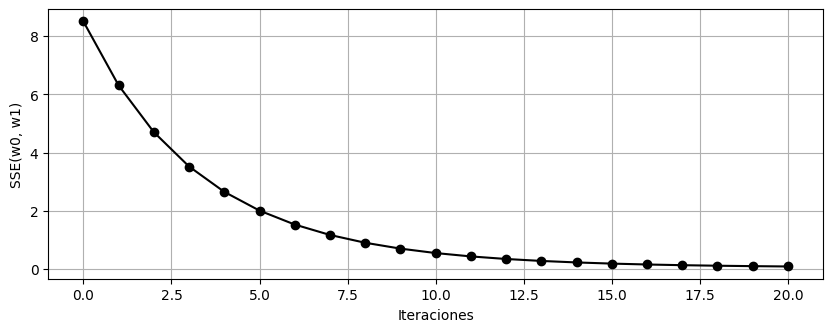
[10]:
plt.figure(figsize=(10, 3.5))
plt.plot(history["sse"], "o-k")
plt.xlabel("Iteraciones")
plt.ylabel("SSE(w0, w1)")
plt.grid()
[11]:
#
# A continuación se grafica la recta encontrada.
#
plt.figure(figsize=(3.5, 3.5))
plot_forecast(w0, w1)