Algoritmos para modificar la tasa de aprendizaje#
Ultima modificación: Feb 01, 2024 | YouTube
Preparación#
[1]:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
Definición del problema#
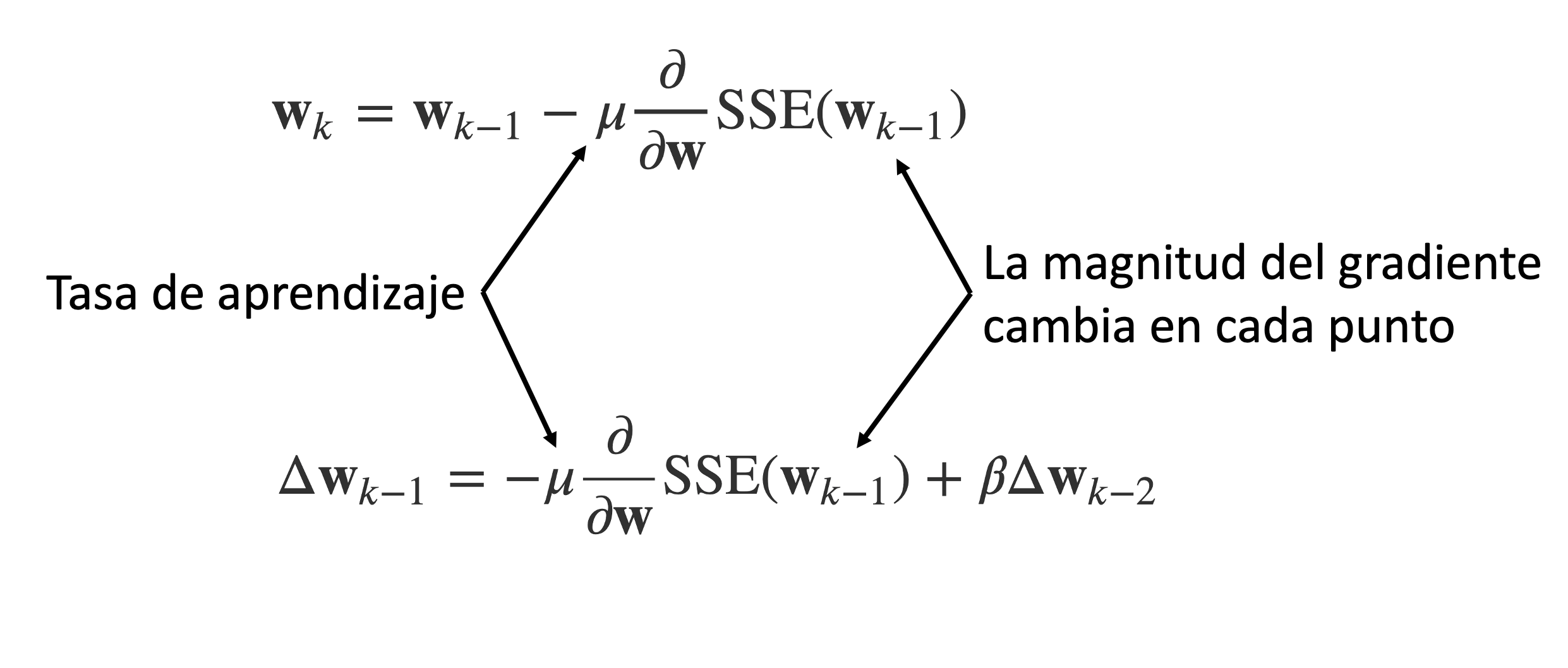
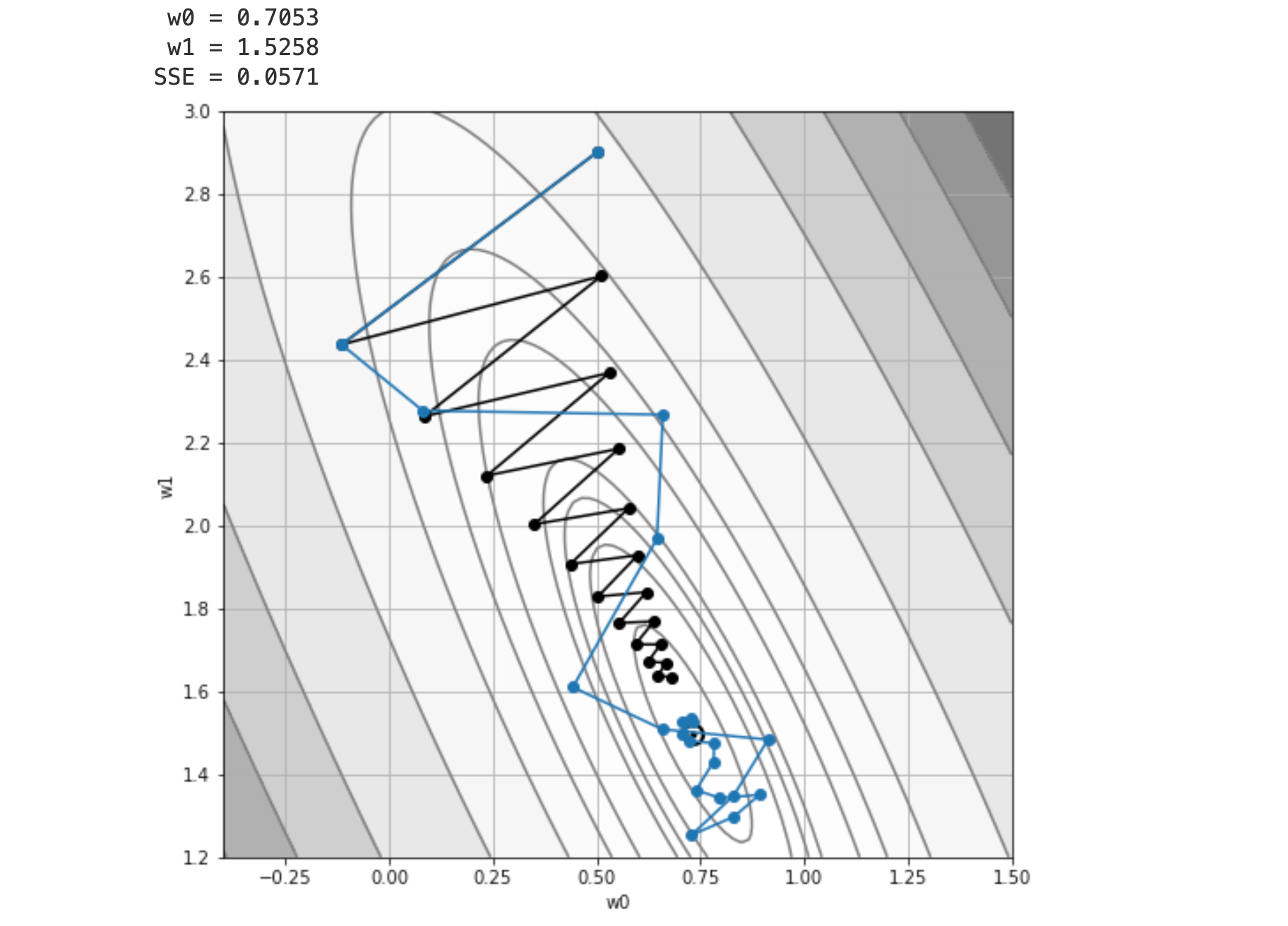
En los métodos del gradiente descendente y la regla delta, la magnitud de los cambios en los parámetros dependen de la magnitud del gradiente en cada punto.
Se desea que la tasa de aprendizaje \mu sea grande para que acelere el avance en regiones lejanas del mínimo.
Se desea que \mu sea pequeño en la cercania del mínimo para evitar que el algoritmo oscile alrededor del punto de mínima y converja a la solución óptima.
Esquemas para modificar la tasa de aprendizaje#
Tasa de aprendizaje constante
En esta estrategia, la tasa de aprendizaje ($ :nbsphinx-math:`mu `$) es constante durante todo el proceso. Corresponde al caso anterior.
Escalado inverso de la tasa de aprendizaje
La tasa de aprendizaje disminuye a medida que se avanza hacia el mínimo, con el fin de poder entrar en la región de influencia del mínimo de aguja y encontra el punto óptimo.
\mu = \frac{\mu_0}{t^n}
[2]:
max_iter = 100
mu0 = 0.1
n = 0.5
mu = [mu0 / (t ** n) for t in range(1, max_iter + 1)]
plt.figure(figsize=(11, 5))
plt.plot(mu, ".-", color="tab:blue", label="delta rule")
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.xlabel("Iteraciones")
plt.ylabel("Tasa de aprendizaje")
plt.show()

Estrategia adaptativa
En esta estrategia la tasa se mantiene constante durante cierto número de iteraciones. Cuando no se puede mejorar el punto actual, la tasa de aprendizaje es dividida por una constante k y se continua con el proceso de optimización.
\mu = \frac{\mu}{k}
[3]:
max_iter = 100
mu0 = 0.1
n = 0.5
mu = [mu0 / (2 ** int(t / 10)) for t in range(1, max_iter + 1)]
plt.figure(figsize=(11, 5))
plt.plot(mu, ".-", color="tab:blue", label="delta rule")
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.xlabel("Iteraciones")
plt.ylabel("Tasa de aprendizaje")
plt.show()

Estrategia óptima
Esta es otra estrategia para disminuir el valor de la tasa de aprendizaje en cada iteración del algoritmo.
\mu = \frac{1}{\alpha(t + t_0)}
t_0 = \frac{1}{\alpha \times \mu_0}
[4]:
max_iter = 100
mu0 = 0.1
alpha = 0.5
t0 = 1 / (alpha * mu0)
mu = [1 / (alpha * (t + t0)) for t in range(1, max_iter + 1)]
plt.figure(figsize=(11, 5))
plt.plot(mu, ".-", color="tab:blue", label="delta rule")
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.xlabel("Iteraciones")
plt.ylabel("Tasa de aprendizaje")
plt.show()

Impacto en la optimización#
[5]:
x_sample = np.array(
[
0.1087,
0.2698,
0.3765,
0.2146,
0.9155,
0.0246,
0.0221,
0.8632,
0.6460,
0.2092,
0.8567,
0.1591,
0.9647,
0.6231,
0.7460,
0.3654,
0.3065,
0.6886,
0.4966,
0.2008,
0.2618,
0.7607,
0.1563,
0.4424,
0.7731,
]
)
y_sample = np.array(
[
0.9519,
1.1237,
1.2360,
1.0526,
2.0743,
0.7906,
0.7603,
2.0533,
1.6887,
1.0563,
2.0991,
0.8953,
2.1917,
1.6266,
1.8508,
1.2828,
1.2283,
1.8722,
1.4657,
1.0418,
1.1097,
1.7826,
0.9711,
1.4267,
1.8248,
]
)
[6]:
def sse(w0, w1):
y_forecasts = [w0 + w1 * x_value for x_value in x_sample]
errors = [y_true - y_forecast for y_true, y_forecast in zip(y_sample, y_forecasts)]
squared_errors = [error ** 2 for error in errors]
return sum(squared_errors)
[7]:
def plot_contour():
W0 = np.linspace(-0.5, 1.5, 100)
W1 = np.linspace(1.0, 3.0, 100)
W0, W1 = np.meshgrid(W0, W1)
F = sse(W0, W1)
levels = [0, 0.2, 0.5, 0.75, 1, 2, 3, 5, 10, 20, 30, 40, 50, 60]
_, ax = plt.subplots(figsize=(3.5, 3.5))
ax.set_aspect("equal", "box")
ax.contourf(W0, W1, F, cmap=cm.Greys, levels=levels, alpha=0.8)
ax.contour(W0, W1, F, colors="gray", levels=levels)
plt.plot(
[0.731],
[1.498],
"o",
color="black",
fillstyle="none",
markersize=11,
markeredgewidth=2,
)
plt.plot([0.731], [1.498], ".", color="black")
ax.set_xlabel("w0")
ax.set_ylabel("w1")
ax.grid()
plot_contour()

[8]:
def gradient(w0, w1):
y_forecasts = [w0 + w1 * x_value for x_value in x_sample]
errors = [y_true - y_forecast for y_true, y_forecast in zip(y_sample, y_forecasts)]
gradient_w0 = -2 * sum(errors)
gradient_w1 = -2 * sum(
[error * x_value for error, x_value in zip(errors, x_sample)]
)
return gradient_w0, gradient_w1
[9]:
def improve(w0, w1, mu):
gradient_w0, gradient_w1 = gradient(w0, w1)
w0 = w0 - mu * gradient_w0
w1 = w1 - mu * gradient_w1
return w0, w1
Comparación entre las metodologías#
[10]:
#
# Punto de inicio
#
history = {}
max_iter = 20
mu0 = 0.03
n = 0.1
alpha = 0.5
t0 = 1 / (alpha * mu0)
plot_contour()
strategies = ["constant", "inverse_scaling", "optimal"]
colors = [
"black",
"tab:blue",
"tab:orange",
]
for i_strategy, strategy in enumerate(strategies):
w0 = 0.5
w1 = 2.9
history["w0"] = [w0]
history["w1"] = [w1]
history[strategy] = [sse(w0, w1)]
for epoch in range(max_iter):
if strategy == "constant":
mu = mu0
if strategy == "inverse_scaling":
mu = mu0 / ((epoch + 1) ** n)
if strategy == "optimal":
mu = 1 / (alpha * (epoch + t0))
w0, w1 = improve(w0, w1, mu)
history["w0"].append(w0)
history["w1"].append(w1)
history[strategy].append(sse(w0, w1))
plt.plot(
history["w0"],
history["w1"],
marker="o",
color=colors[i_strategy],
label=strategy,
)
plt.legend()
plt.show()

[11]:
plt.figure(figsize=(10, 3.5))
for i_strategy in range(len(strategies)):
plt.plot(
history[strategies[i_strategy]],
"o-",
color=colors[i_strategy],
label=strategies[i_strategy],
)
plt.xlabel("Iteraciones")
plt.ylabel("SSE(w0, w1)")
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.legend()
plt.show()
