Aprendizaje Mini-batch#
Ultima modificación: Feb 01, 2024 | YouTube
Definición del problema de estimación de parámetros y función de pérdida#
Se desean encontra los parámetros w_0 y w_1 del siguiente modelo de regresión entre las variables x y y:
y_i = w_1 x_i + w_0 + e_i
a partir de un conjunto de observaciones \{d_i, x_i\}, donde d_i es el valor real (observado), y_i es su aproximación usando el modelo de regresión descrito, y e_i es el error.
Error instantáneo:
e_i = d_i - y_i
Sumatoria del error cuadrático instantáneo:
\begin{split} \text{SSE}(w_0, w_1) & = \sum_i (d_i - y_i)^2 \\ & = \sum_i e_i^2 \end{split}
Método del gradiente#
Aprendizaje Online:
\mathbf{w}_k = \mathbf{w}_{k-1} - \mu \left( \frac{\partial}{\partial \mathbf{w}} e_i^2 \right)
Aprendizaje Batch:
\begin{split} \mathbf{w}_k & = \mathbf{w}_{k-1} - \mu \sum_i \left( \frac{\partial}{\partial \mathbf{w}} e_i^2 \right) \end{split}
Minibatch#
Para conjuntos de datos muy grandes el aprendizaje batch es muy costoso computacionalmente ya que deben recorrerse todos los datos, mientras que el aprendizaje online es muy lento en converger. Es en este caso, donde se toma un punto intermedio:
El conjunto de datos se divide en varios subconjuntos.
Se ordenan aleatoriamente los subconjuntos de datos y luego se recorren uno a uno, tal como en el caso del gradiente descendente estocástico.
Para el subconjunto actual, se computa el gradiente neto (tal como en el caso del aprendizaje batch) y se corrigen los parámetros.
Se repite nuevamente el proceso hasta que el algoritmo converga.
Implementación#
[1]:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
[2]:
#
# Dataset
#
x_sample = [
0.1087,
0.2698,
0.3765,
0.2146,
0.9155,
0.0246,
0.0221,
0.8632,
0.6460,
0.2092,
0.8567,
0.1591,
0.9647,
0.6231,
0.7460,
0.3654,
0.3065,
0.6886,
0.4966,
0.2008,
0.2618,
0.7607,
0.1563,
0.4424,
0.7731,
]
y_sample = [
0.9519,
1.1237,
1.2360,
1.0526,
2.0743,
0.7906,
0.7603,
2.0533,
1.6887,
1.0563,
2.0991,
0.8953,
2.1917,
1.6266,
1.8508,
1.2828,
1.2283,
1.8722,
1.4657,
1.0418,
1.1097,
1.7826,
0.9711,
1.4267,
1.8248,
]
[3]:
#
# Función auxiliar para computar el SSE
#
#
# Sumatoria del error cuadrático o pérdida cuadrática
#
def sse(w0, w1):
y_forecasts = [w0 + w1 * x_value for x_value in x_sample]
errors = [y_true - y_forecast for y_true, y_forecast in zip(y_sample, y_forecasts)]
squared_errors = [error ** 2 for error in errors]
return sum(squared_errors)
[4]:
#
# Función auxililar para graficar el contorno
#
def plot_contour():
W0 = np.linspace(0.0, 2.0, 50)
W1 = np.linspace(1.5, 3.2, 50)
W0, W1 = np.meshgrid(W0, W1)
F = sse(W0, W1)
levels = [0, 0.2, 0.5, 0.75, 1, 2, 3, 5, 10, 20, 40, 60, 80, 100, 120]
fig, ax = plt.subplots(figsize=(3.5, 3.5))
ax.set_aspect("equal", "box")
ax.contourf(W0, W1, F, cmap=cm.Greys, levels=levels, alpha=0.8)
ax.contour(W0, W1, F, colors="gray", levels=levels)
ax.grid()
ax.set_xlabel("w0")
ax.set_ylabel("w1")
Cómputo del gradiente en el algoritmo minibatch y función de mejora#
[5]:
#
# Esta es el mismo computo que el empleado en el
# método batch.
#
def gradient(w0, w1, indices):
x_batch = x_sample[indices]
y_batch = y_sample[indices]
y_forecasts = [w0 + w1 * x_value for x_value in x_batch]
errors = [y_true - y_forecast for y_true, y_forecast in zip(y_batch, y_forecasts)]
gradient_w0 = -2 * sum(errors)
gradient_w1 = -2 * sum([error * x_value for error, x_value in zip(errors, x_batch)])
return gradient_w0, gradient_w1
[6]:
def improve(w0, w1, mu, indices):
gradient_w0, gradient_w1 = gradient(w0, w1, indices)
w0 = w0 - mu * gradient_w0
w1 = w1 - mu * gradient_w1
return w0, w1
Particionamiento de los grupos#
[7]:
n_batches = 5
batch_indices = np.array_split(np.array(range(len(x_sample))), n_batches)
batch_indices
[7]:
[array([0, 1, 2, 3, 4]),
array([5, 6, 7, 8, 9]),
array([10, 11, 12, 13, 14]),
array([15, 16, 17, 18, 19]),
array([20, 21, 22, 23, 24])]
Ejecución del algoritmo#
[8]:
#
# Punto de inicio
#
w0 = 0.5
w1 = 3.0
history = {
"w0": [w0],
"w1": [w1],
"sse": [sse(w0, w1)],
}
mu = 0.05
x_sample = np.array(x_sample)
y_sample = np.array(y_sample)
for epoch in range(10):
for i_group in np.random.choice(n_batches, n_batches, replace=False):
indices = list(batch_indices[i_group])
w0, w1 = improve(w0, w1, mu, indices)
history["w0"].append(w0)
history["w1"].append(w1)
history["sse"].append(sse(w0, w1))
print(" w0 = {:6.4f}\n w1 = {:6.4f}\nSSE = {:6.4f}\n".format(w0, w1, sse(w0, w1)))
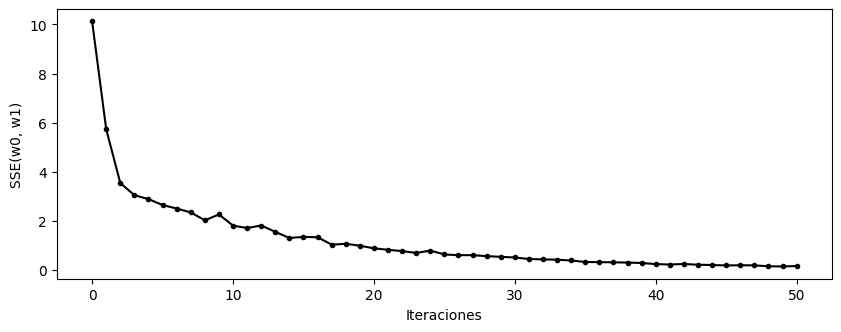
plot_contour()
plt.plot(history["w0"], history["w1"], marker=".", color="black")
plt.show()
w0 = 0.6576
w1 = 1.7088
SSE = 0.1586
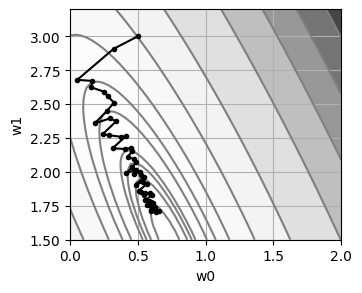
[9]:
plt.figure(figsize=(10, 3.5))
plt.plot(history["sse"], ".-k")
plt.xlabel("Iteraciones")
plt.ylabel("SSE(w0, w1)")
plt.show()