Definición de probabilidad como frecuencia#

  • El espacio muestral se define como el conjunto S de todos los posibles resultados de un experimento.

  • Un evento x_i es cualquier colección de posibles resultados de un experimento (subconjunto del espacio muestral).

  • La probabilidad es la frecuencia con que ocurren un evento.

Por ejempo, si en la tirada de dos dados se definen como un evento la suma de los puntos obtenidos, entonces:

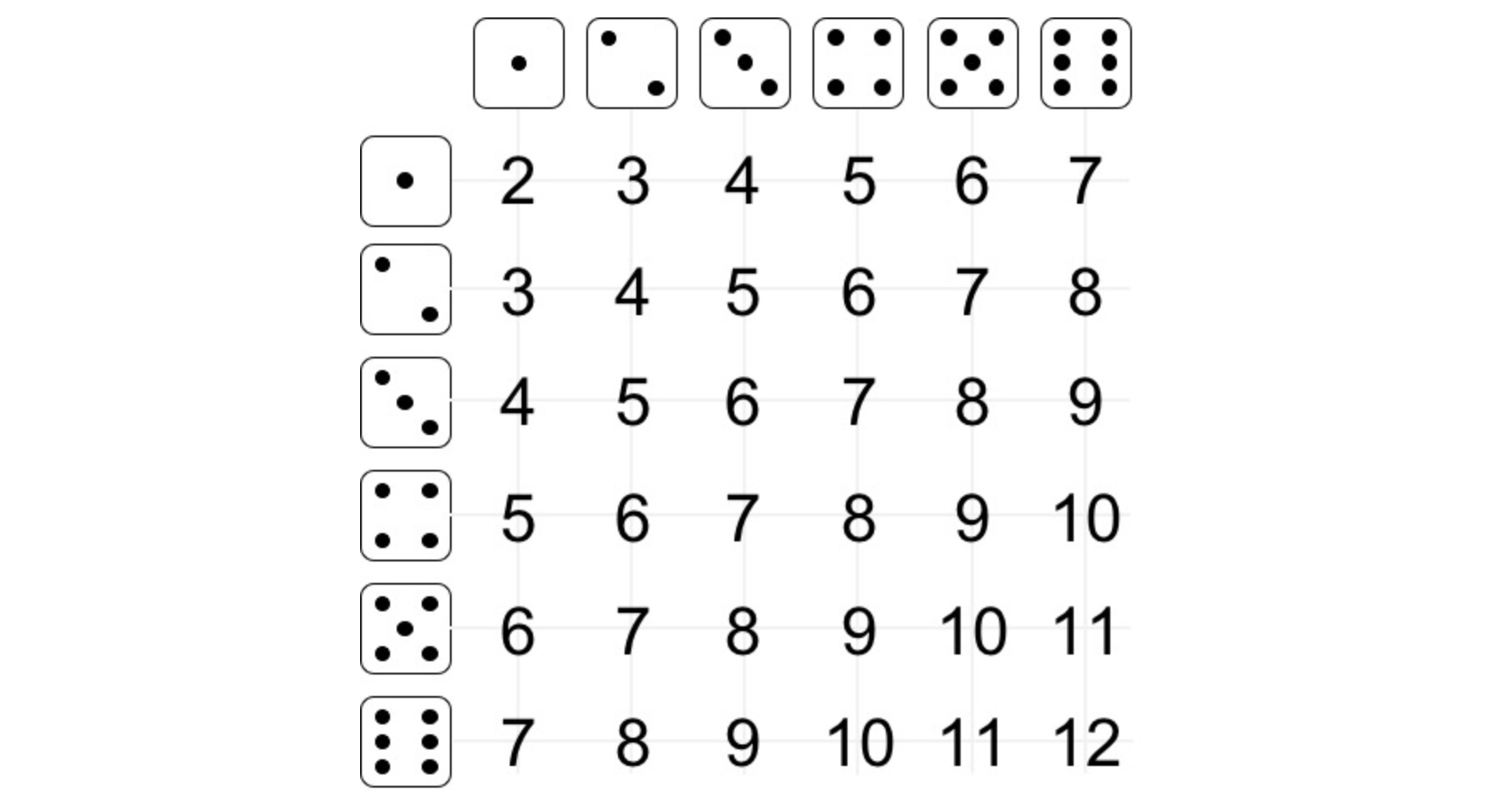
tirada-dados

Pr(𝑋= 2) = 1 / 36   Pr(𝑋= 6) = 5 / 36   Pr(𝑋=10) = 3 / 36
Pr(𝑋= 3) = 2 / 36   Pr(𝑋= 7) = 6 / 36   Pr(𝑋=11) = 2 / 36
Pr(𝑋= 4) = 3 / 36   Pr(𝑋= 8) = 5 / 36   Pr(𝑋=12) = 1 / 36
Pr(𝑋= 5) = 4 / 36   Pr(𝑋= 9) = 4 / 36

Pregunta.— Los soldados mediavales apostaban con dos dados de la siguiente manera: si el resultado es par {2, 4, 6, 8, 10, 12} ganaba el soldado A; y si el resultado es impar {3, 5, 7, 9, 11} ganaba el soldado B. ¿Quién tiene mayor probabilidad de ganar?

  • Las probabilidades deben cumplir con las siguientes propiedades:

    • Todas las probabilidades deben estar entre 0 y 1:

    0 \le \text{Pr}(x_i) \le 1

    • Las probabilidades de eventos mutuamente exclusivos (no pueden ocurrir simultáneamente) y colectivamente exhaustivos (cubren todo el universo de casos posibles) deben sumar la unidad:

    \sum_{i=1}^n \text{Pr}(x_i) = 1

En las siguientes figuras, los eventos F1, F2 y F3, y V1 y V2 están definidos sobre el mismo universo; y son mutuamente exclusivos y colectivamente exhaustivos, tal que se cumplen las dos propiedades anteriores. Para facilidad de interpretación, se definen:

F1: Tener camisa amarilla
F2: Tener camisa roja
F3: Tener camisa negra

V1: Tener tenis azules
V2: Tener tenis grises

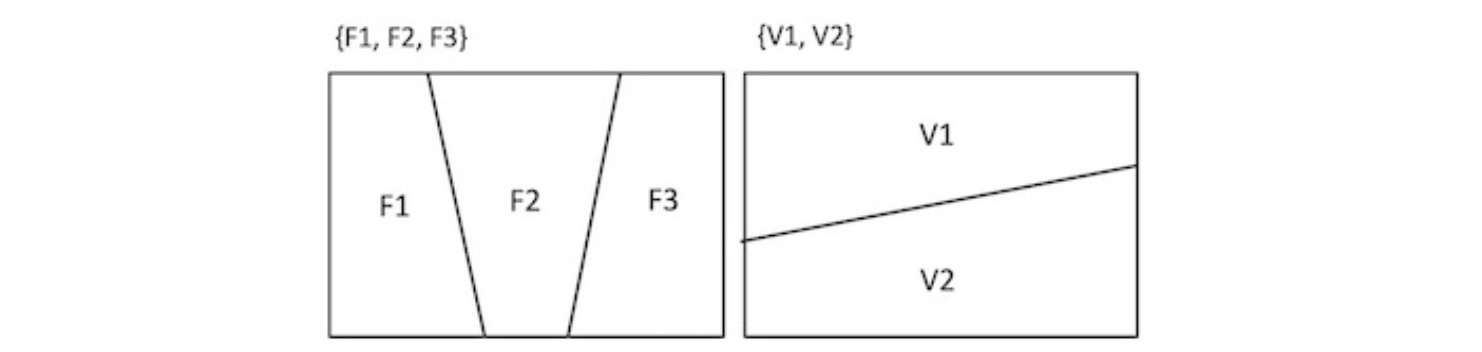
assets/eventos-conjuntos-2.jpg

\text{Pr}(F1) + \text{Pr}(F2) + \text{Pr}(F3) = 1, \quad \qquad \text{Pr}(V1) + \text{Pr}(V2) = 1