Distribución Binomial

• La distribución binomial se obtiene al considerar una secuencia de n experimentos independientes de Bernoulli en los que se obtienen exactamente Y éxitos, es decir, ocurre X=1, y veces.

• En otras palabras, si se tiene una secuencia de n experimentos idénticos, cada uno con una probabilidad de éxito p, y se definen las variables aleatorias X_1, …, X_n como:

  X_i = \begin{cases} 1, & \text{con probabilidad $p$} \\ 0, &\text{con probabilidad $1-p$} \end{cases}

  entonces, la variable aleatoria

  Y = \sum_{i=1}^n X_i

  sigue una distribución binomial(n, p).

---

import numpy as np

#
# Simulación del número de exitos en 5 tiradas de
# una moneda
#
np.random.binomial(5, 0.5)

3

#
# Simulación del número de éxitos en 5 tiradas de
# una moneda repetido 10 veces.
#
np.random.binomial(5, 0.5, 10)

array([4, 2, 3, 3, 3, 2, 2, 2, 1, 4])

---

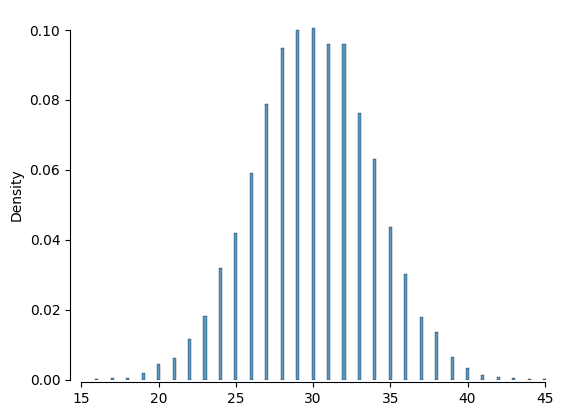
• Con una cantidad de experimentos n suficientemente grande, y si p no es muy cercano a 0 o 1, la distribución binomial puede ser aproximada por una distribución normal.

---

import matplotlib.pyplot as plt
import seaborn as sns

#
# Función de densidad de probabilidad simulada
#
samples = np.random.binomial(60, 0.5, 10000)
sns.histplot(samples, discrete=True, shrink=0.2, stat="density")
sns.despine(trim=True, offset=2)
plt.show()