Bootstrap — 24:53 min#
24:53 min | Ultima modificación: Marzo 31, 2021 | YouTube
El boostrap es una técnica numérica que permite estimar la distribución muestral de un estadístico.
El bootstrap se usa cuando no es posible derivar ecuaciones que permitan aproximar la distribución de probabilidades de un estadístico.
En el bootstrap siempre aplica muestreo con reemplazo.
El remuestreo también incluye permutaciones combinando varias muestras, posiblemente sin reemplazo.
Una muestra bootstrap es una muestra con reemplazo obtenida de la muestra original.
Suponga que tiene una muestra de ocho ejemplos:
\{x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8\}
Una muestra bootstap se obtiene de la muestra original, seleccionando ocho elementos de forma aleatoria con reemplazo. Por ejemplo, una muestra bootstrap podría ser:
\{x_1, x_2, x_2, x_2, x_4, x_1, x_7, x_7\}
Nóte que los elementos pueden repetirse.
Boostrap no paramétrico:
Se tiene la muestra x=\{x_i; 1,...,n\}, que en ese caso es \{x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8\} con n=8.
Se seleccionan B muestras bootstrap independientes x^{*1}, ..., x^{*B} cada una de n elementos obtenidos de la muestra original. Por ejemplo:
\begin{split} \\ x^{*1} & = \{x_1, x_2, x_2, x_2, x_4, x_1, x_7, x_7\} \\ \\ x^{*2} & = \{x_4, x_1, x_2, x_4, x_8, x_3, x_1, x_1\} \\ \\ x^{*3} & = \{x_7, x_7, x_1, x_3, x_6, x_1, x_4, x_8\} \end{split}
y así sucesivamente.
Para cada muestra bootstap se calcula el estadístico de interes: \theta(b) = t(x^{*b}). Es decir:
\begin{split} \\ \theta(1) & = t(x^{*1}) = t(\{x_1, x_2, x_2, x_2, x_4, x_1, x_7, x_7\}) \\ \\ \theta(2) & = t(x^{*2}) = t(\{x_4, x_1, x_2, x_4, x_8, x_3, x_1, x_1\}) \\ \\ \theta(3) & = t(x^{*3}) = t(\{x_7, x_7, x_1, x_3, x_6, x_1, x_4, x_8\}) \end{split}
y así sucesivamente.
La muestra \theta(1), ..., \theta(B) representa la distribución de probabilidades de \theta y puede calcularsele valor esperado, desviación estándar, etc. El valor buscado sería:
\bar{\theta}(\bullet) = \frac{1}{B} \sum_{b=1}^B \theta (b)
El error estándar se puede calcular como:
\text{se}_B = \left\{ \frac{1}{B-1} \sum_{b=1}^B \left[\theta(b) - \bar{\theta}(\bullet) \right]^2 \right\}^{(1/2)}
Se desea obtener una aproximación a la media poblacional a partir de la siguiente muestra:
[1]:
x = [0.09, 0.15, 0.18, 0.16, 0.23, 0.35, 0.49, 0.68, 0.71, 0.85, 0.96, 0.98, 0.27]
[2]:
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
from sklearn.utils import resample
[3]:
#
# La función resample permite hacer un muestreo con reemplazo.
#
boot = resample(
x, # muestra
replace=True, # reemplazo?
n_samples=len(x), # longitud de la nueva muestra
random_state=None,
) # generador de aleatorios
boot
[3]:
[0.98, 0.23, 0.71, 0.98, 0.15, 0.09, 0.18, 0.35, 0.98, 0.35, 0.16, 0.09, 0.85]
[4]:
##
## Se generan 500 muestras bootstrap
##
sample = [resample(x, replace=True, n_samples=len(x)) for _ in range(500)]
sample[0:2]
[4]:
[[0.35,
0.18,
0.18,
0.68,
0.71,
0.49,
0.15,
0.49,
0.09,
0.18,
0.16,
0.09,
0.23],
[0.27,
0.35,
0.68,
0.18,
0.16,
0.49,
0.23,
0.98,
0.35,
0.23,
0.96,
0.49,
0.09]]
[5]:
#
# Se computa la media para cada muestra bootstrap
#
stat = [np.mean(s) for s in sample]
stat[0:5]
[5]:
[0.30615384615384617,
0.42,
0.5015384615384616,
0.38384615384615384,
0.3253846153846153]
[6]:
#
# Estimado de la media de la población
#
np.mean(stat)
[6]:
0.46413846153846156
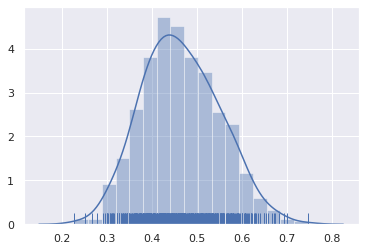
[7]:
#
# Histograma de las medias calculadas
#
sns.set(color_codes=True)
sns.distplot(stat, rug=True)
plt.show()
[8]:
#
# Error estándar (desviación estándar) para
# el valor computado de la media
#
np.std(stat)
[8]:
0.08591046529577916
Distribución de probabilidades del estadístico boostrap:
Se obtiene aplicando el teorema del límite central: Si s_1, …, s_n es una muestra aleatoria donde las observaciones s_i son independientes e identicamente distribuidas de una distribución con media \mu y varianza finita \sigma^2, entonces:
\bar{s} = \frac{1}{n} \sum_{i=1}^n s_i
sigue una distribución normal con media \mu y varianza (\sigma_{\bar{s}})^2 = \sigma^2 / n.
Para el algoritmo boostrap, s_i = \theta(i), lo que quiere decir que $ \theta`(i)$ sigue una distribución normal :math:`N(\mu, \sigma) con:
\begin{split} \mu & = \bar{\theta}(\bullet) \\ \\ & = \frac{1}{B} \sum_{b=1}^B \theta (b) \end{split}
y
\begin{split} \sigma & = \text{se}_B \\ \\ & = \left\{\frac{1}{B-1} \sum_{b=1}^B \left[\theta(b) - \bar{\theta}(\bullet) \right]^2 \right\}^{(1/2)} \end{split}
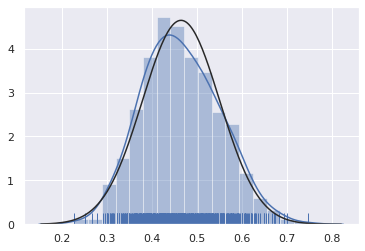
[9]:
#
# Distribución normal teórica
#
sns.set(color_codes=True)
sns.distplot(stat, rug=True, fit=stats.norm)
plt.show()
[10]:
#
# Intervalos de confianza para +/- 2 sigma
# aprox el 95% de confianza
#
[np.mean(stat) - 2 * np.std(stat), np.mean(stat) + 2 * np.std(stat)]
[10]:
[0.29231753094690327, 0.6359593921300198]
Jacknife:
Se obtiene al dejar un solo elemento fuera de la muestra de datos.
Se tiene la muestra x=\{x_i; 1,...,n\}, que en ese caso es \{x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8\} con n=8.
Se obtienen n muestras jackknife x_{(i)}, i=1, ...,n, donde:
\begin{split} \\ x_{(i)} & = (x_1, \; x_2, \; ..., \; x_{i-1}, \; x_{i+1}, \; ..., \; x_n) \end{split}
Es decir:
\begin{split} \\ x_{(1)} & = (x_2, \; x_3, \; x_4, \; ..., \; x_{7}, \; x_{8}) \\ \\ x_{(2)} & = (x_1, \; x_3, \; x_4, \; ..., \; x_{7}, \; x_{8}) \\ \\ x_{(3)} & = (x_1, \; x_2, \; x_4, \; ..., \; x_{7}, \; x_{8}) \\ \\ ... \\ \\ x_{(8)} & = (x_1, \; x_2, \; x_3, \; ..., \; x_{6}, \; x_{7}) \\ \\ \end{split}
Se calcula el estadístico para la muestra jackknife:
\begin{split} \theta_{(i)} = t(x_{(i)}) \\ \end{split}
que para la muestra actual es:
\begin{split} \theta_{(1)} & = t(x_{(1)}) \\ \\ \theta_{(2)} & = t(x_{(2)}) \\ \\ ... \\ \\ \theta_{(8)} & = t(x_{(8)}) \\ \\ \end{split}
El error estándar se obtiene como:
\text{se}_{\text{jack}} = \left\{ \frac{n-1}{n} \sum_{i=1}^n \left[ \theta_{(i)} - \theta_{(\bullet)} \right]^2 \right\}^{1/2}
\bar{\theta}(\bullet) = \frac{1}{n} \sum_{i=1}^n \theta_{(i)}