La distribución normal

• La distribución normal fue esencial en el desarrollo histórico de la estadísitca, ya que permitio una aproximación matemática de la incertidumbre y la variabilidad. Consulte su historia en Wikipedia.

• Usualmente los datos en bruto no son normalmente distribuidos, pero los errores si lo son, así como los promedios y los totales sobre grandes muestras.

• La función de densidad de probabilidad de una distribución normal con media \mu y varianza \sigma^2 se define como:

f(x | \mu, \sigma^2) =\frac{1}{\sigma \sqrt{2\pi}} \exp \left\{ -\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2} \right\}

• Los momentos de una istribución normal son:

  • M_1 = \mu

  • M_2 = \sigma^2

  • M_3 = 0

  • M_4 = 3\sigma^2

---

En la siguiente figura se observan diferentes distribuciones normales que varian en su media y varianza.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

plt.figure(figsize=(8, 6))
x = np.linspace(-4, +4, 100)
plt.plot(x, norm.pdf(x, loc=0.0, scale=np.sqrt(0.2)), "r-", lw=2, alpha=0.6, label="")
plt.plot(
    x, norm.pdf(x, loc=-2.0, scale=np.sqrt(0.5)), "b-", lw=2, alpha=0.6, label=""
)
plt.plot(x, norm.pdf(x, loc=0.0, scale=np.sqrt(1.0)), "k-", lw=2, alpha=0.6, label="")
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.show()

---

Propiedades útiles:

• Sean x \sim \text{N}(\mu_x, \sigma^2_x) y y \sim \text{N}(\mu_y, \sigma^2_y), entonces:

  x + y \sim \text{N}\left(\mu_x + \mu_y, \sigma_x^2 + \sigma_y^2\right)

• Sea x \sim \text{N}(\mu_x, \sigma^2_x) y los números reales arbitrarios a y b, entonces:

ax + b \sim \text{N}\left(a \mu_x + b, a^2 \sigma_x^2\right)

• Sean x \sim \text{N}(\mu_x, \sigma^2_x) y \varepsilon \sim \text{N}(0, 1^2), entonces:

x \sim \mu + \sigma \varepsilon

---

Distribución Normal Estándar

• La distribución normal estándar se obtiene al hacer \mu=0 y \sigma=1 en la distribución normal:

f(z) =\frac{1}{\sqrt{2\pi}} \exp \left\{ -\frac{1}{2} z^2 \right\}

• La estandarización se define como:

  z = \frac{x-\mu}{\sigma}

• Los intevalos de confianza corresponden a los valores de x para los cuales el área central de la normal es igual al porcentaje especificado. En la imagen presentada a continuación se grafican los intervalos de confianza para \pm \; 3 \sigma, \pm \; 2 \sigma y \pm \; \sigma, que equivalen a áreas del 99.73%, 95.44% y 68.26% respectivamente.

---

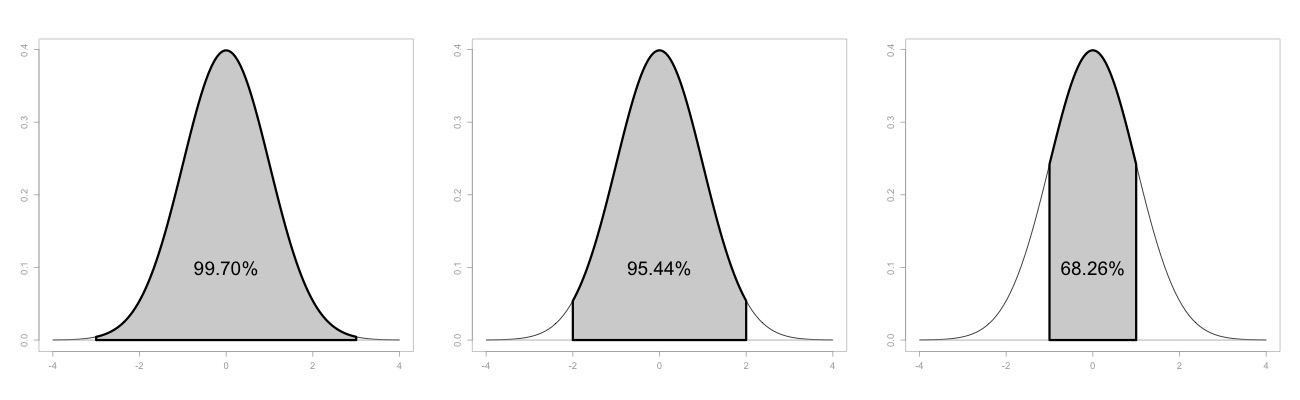
Los valores del área para cada caso se calcularían asi:

# para +/- 3 * sigma
1.0 - 2 * norm.cdf(-3)

0.9973002039367398

# para +/- 2 * sigma
1.0 - 2 * norm.cdf(-2)

0.9544997361036416

# para +/- 1 * sigma
1.0 - 2 * norm.cdf(-1)

0.6826894921370859

---

Gráfico QQ:

• Es una gráfica que permite determinar visualmente que tan cercanos son los datos a una distribución teorica (usualmente la normal).

from scipy.stats import probplot

sample = norm.rvs(size=100)
_ = probplot(sample, plot=plt.gca())