Análisis de Relaciones#
Última modificación: Mar 11, 2024 | YouTube
[1]:
import warnings
warnings.filterwarnings("ignore")
[2]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
Definición del problema#
El conjunto de datos de la flor Iris contiene 150 muestras de las medidas del ancho y el largo del pétalo y del sépalo para las tres especies de esta flor (Iris setosa, Iris virginica e Iris versicolor). A partir de la muestra de datos se desean responder la siguiente pregunta:
P4.— ¿Qué relación existe entre el largo y el ancho del pétalo y el sépalo?
Carga de datos#
[3]:
#
# Se cargan los datos y se realiza una inspección
# inicial de la tabla y los datos
#
iris = sns.load_dataset("iris")
display(iris.head(), iris.tail())
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
Análisis#
[4]:
iris_melt = pd.melt(
iris,
id_vars="species",
var_name="Variables",
value_name="Values",
)
[5]:
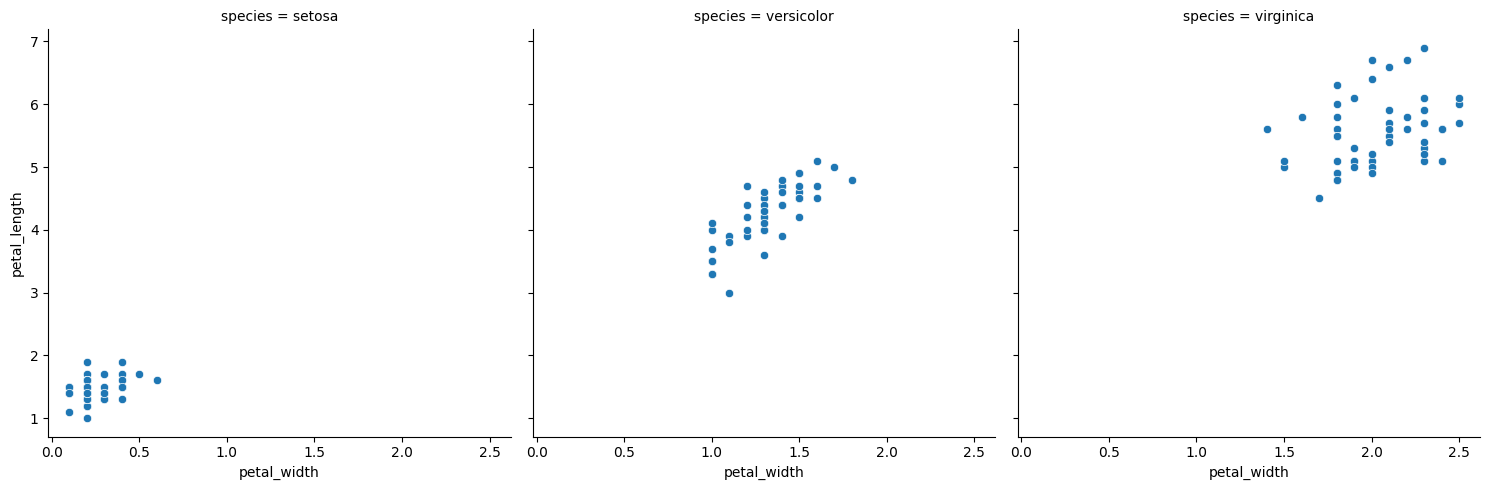
sns.relplot(
x="petal_width",
y="petal_length",
col="species",
data=iris,
)
plt.show()
[6]:
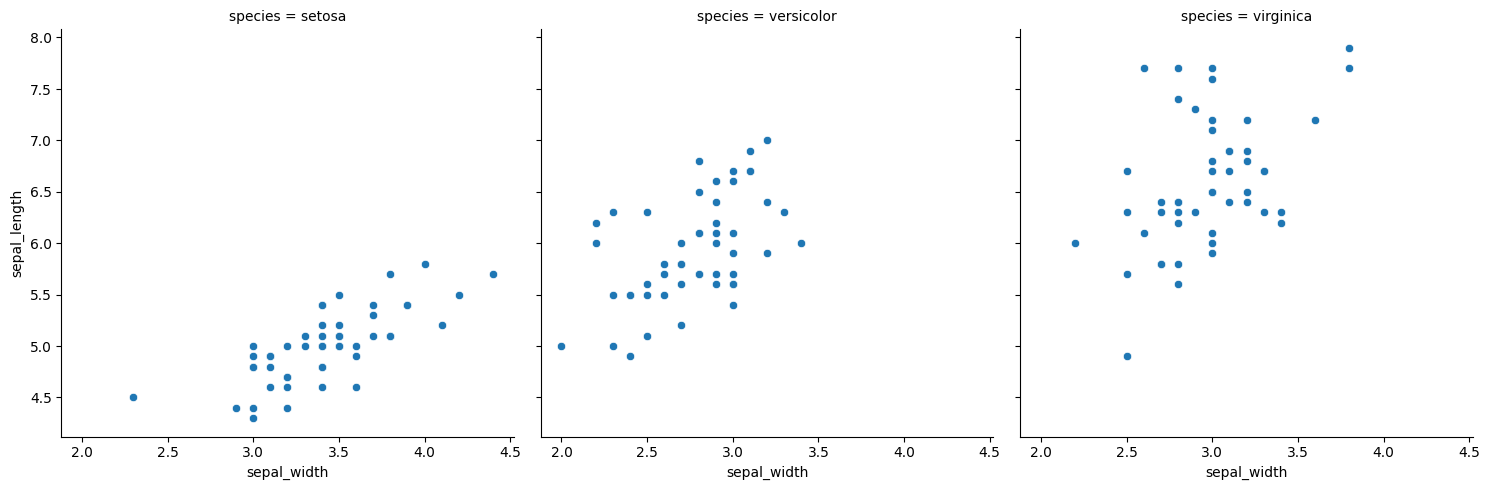
sns.relplot(
x="sepal_width",
y="sepal_length",
col="species",
data=iris,
)
plt.show()
[7]:
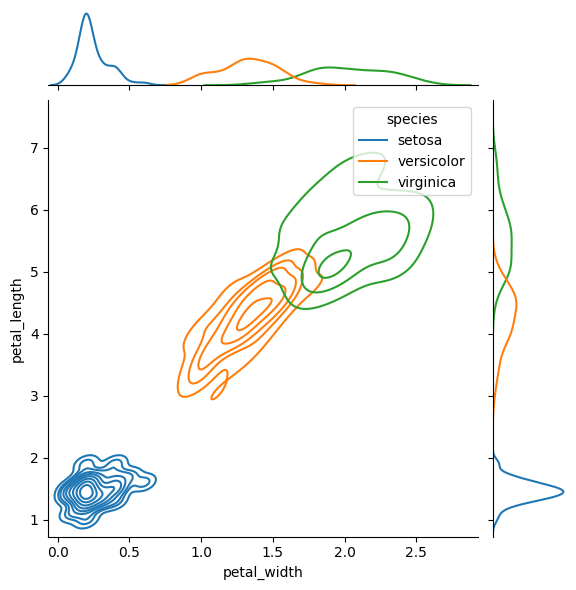
sns.jointplot(
data=iris,
x="petal_width",
y="petal_length",
hue="species",
kind="kde",
)
plt.show()
[8]:
sns.jointplot(
data=iris,
x="sepal_width",
y="sepal_length",
hue="species",
kind="kde",
)
plt.show()
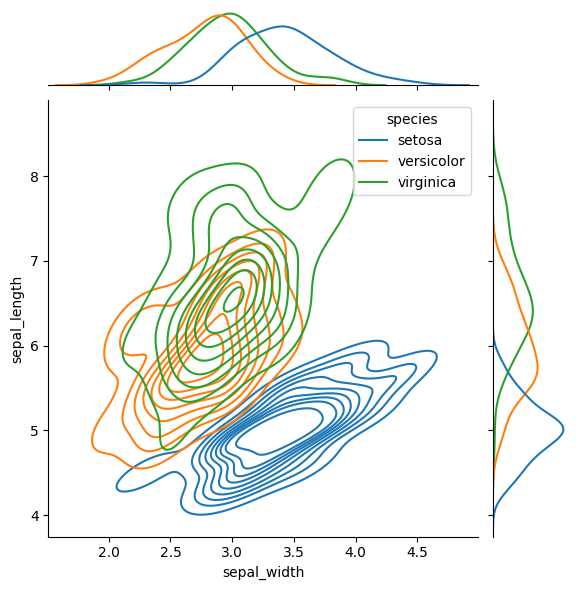
Covarianza
\text{Cov}(x, y) = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y})
[9]:
np.cov(iris.petal_length, iris.sepal_length)
[9]:
array([[3.11627785, 1.27431544],
[1.27431544, 0.68569351]])
[10]:
iris.cov(numeric_only=True)
[10]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 0.685694 | -0.042434 | 1.274315 | 0.516271 |
| sepal_width | -0.042434 | 0.189979 | -0.329656 | -0.121639 |
| petal_length | 1.274315 | -0.329656 | 3.116278 | 1.295609 |
| petal_width | 0.516271 | -0.121639 | 1.295609 | 0.581006 |
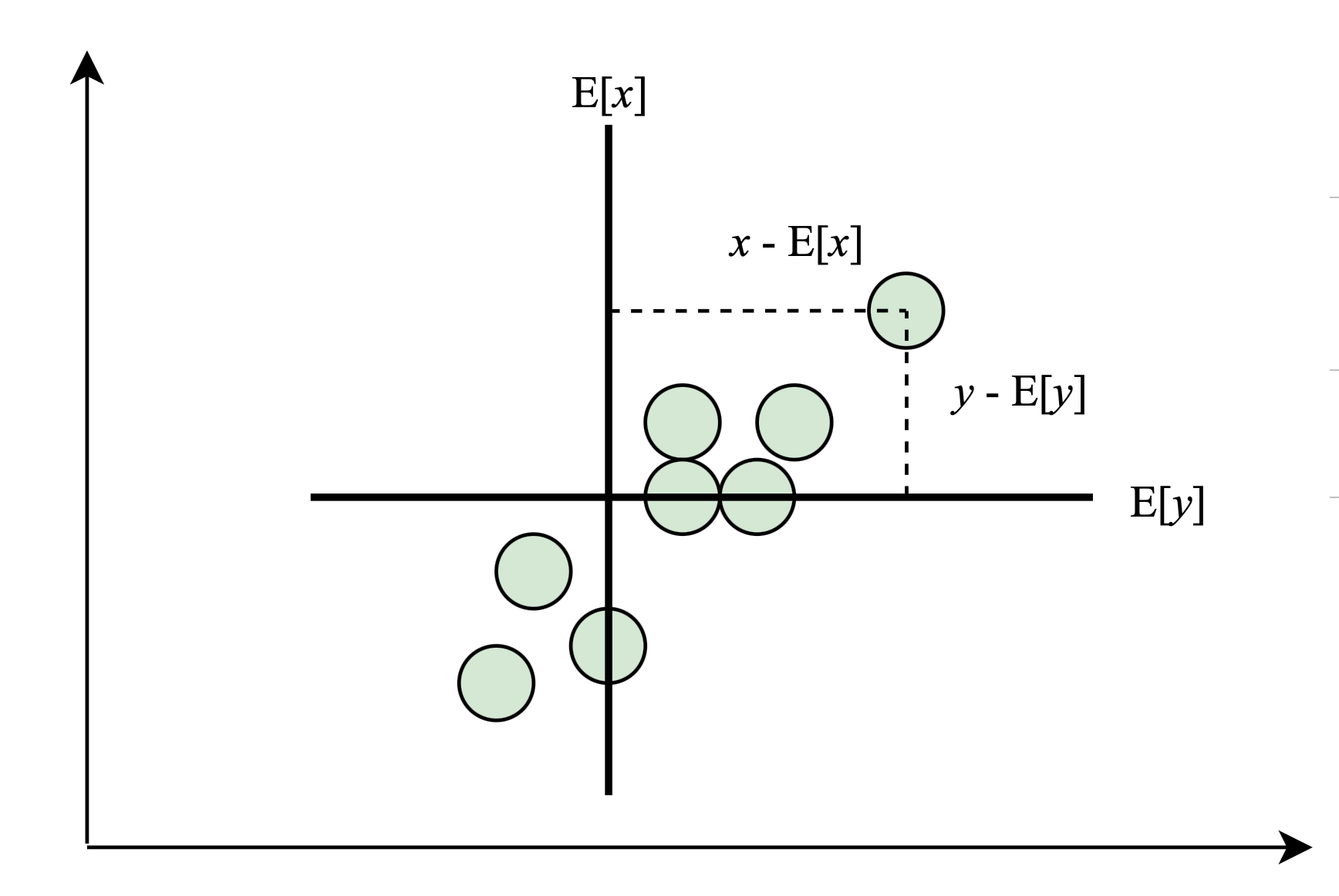
Coeficiente de correlación
Métrica que representa la dependencia entre una variable y otra. El coeficiente de correlación de Pearson r entre dos variables x y y se calcula como:
r=\frac{\sum_{i=1}^n (x_i - \bar{x}) (y_i - \bar{y})} {(n-1)\; s_X \; s_Y}
La correlación va entre -1 (correlación perfecta negativa) y +1 (correlación perfecta positiva). Un valor de 0 indica que no hay correlación.
[11]:
np.corrcoef(iris.sepal_length, iris.petal_length)
[11]:
array([[1. , 0.87175378],
[0.87175378, 1. ]])
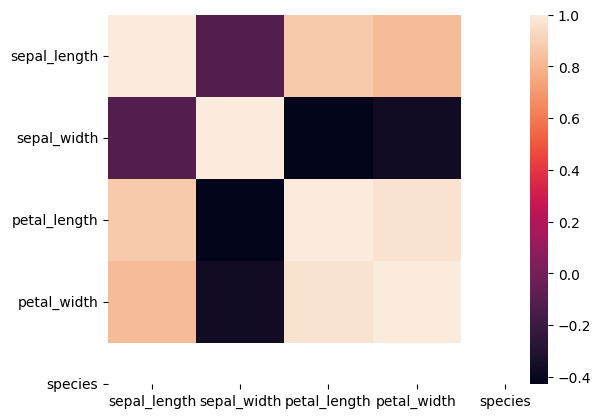
Matriz de correlación
Matriz donde cada fila y cada columna corresponde a una variable, y los elementos corresponden a la correlación entre las respectivas variables.
[12]:
iris.corr(numeric_only=True)
[12]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal_width | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal_length | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal_width | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
[13]:
sns.heatmap(
iris.corr(numeric_only=True),
xticklabels=iris.columns.values,
yticklabels=iris.columns.values,
)
plt.show()
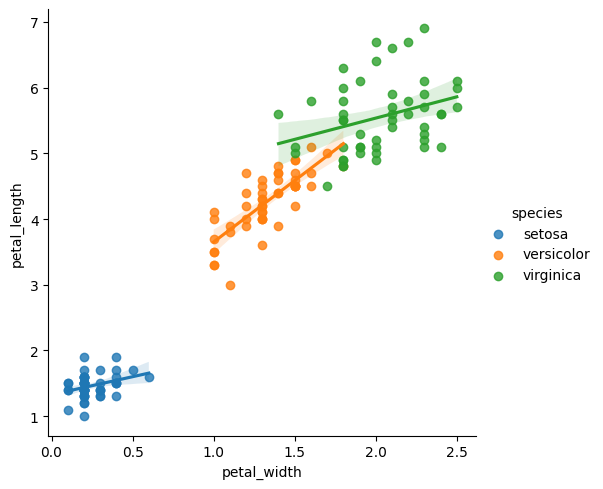
Regresión
[14]:
sns.lmplot(
x="petal_width",
y="petal_length",
data=iris,
hue="species",
)
plt.show()
[15]:
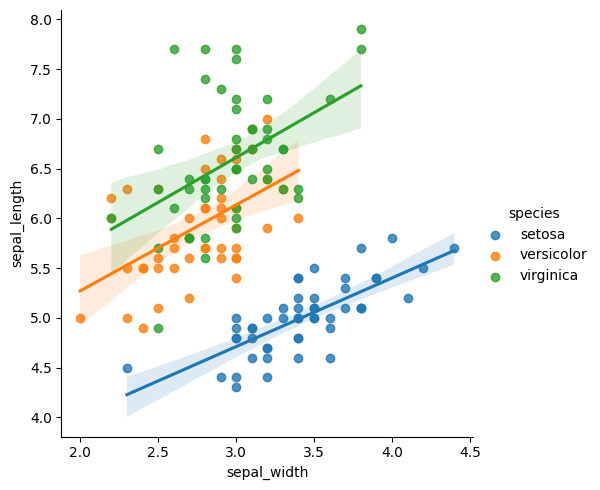
sns.lmplot(
x="sepal_width",
y="sepal_length",
data=iris,
hue="species",
)
plt.show()