Proyecciones aleatorias#
Son métodos eficientes para reducir la dimensionalidad de los datos que intentan conservar al máximo las propiedades de estos.
La proyección gaussiana aleatoria reduce el espacio original de caracaterísticas con una matriz generada aleatoriamente, cuyos elementos son muestreados de una distribución normal:
N \left( 0, \frac{1}{n_\text{components}} \right)
[1]:
import numpy as np
from sklearn.random_projection import GaussianRandomProjection
X = np.random.rand(100, 10000)
gaussianRandomProjection = GaussianRandomProjection(
# -----------------------------------------------------
# Dimensionality of the target projection space.
# int
# 'auto'
n_components="auto",
# -----------------------------------------------------
# Semilla del generador de aleatorios
# None
# int
random_state=1234,
)
X_new = gaussianRandomProjection.fit_transform(X)
X_new.shape
[1]:
(100, 3947)
[2]:
#
# Número de componentes
#
gaussianRandomProjection.n_components_
[2]:
3947
[3]:
#
# Componentes
#
gaussianRandomProjection.components_.shape
[3]:
(3947, 10000)
En la proyección aleatoria dispersa se reduce la dimensionalidad de la muestra de datos usando una matriz aleatoria dispersa. Esta alternativa es más eficiente que la anterior. Los elementos de la matriz son muestreados de:
\begin{cases} - \sqrt{\frac{s}{n_\text{components}}} & \text{ con probabilidad } 1/2s \\ 0 & \text{ con probabilidad } 1 - \frac{1}{s} \\ + \sqrt{\frac{s}{n_\text{components}}} & \text{ con probabilidad } 1/2s \\ \end{cases}
donde
s = \frac{1}{\text{density}}
y
\text{density} \propto \frac{1}{\sqrt{n_\text{features}}}
[4]:
import numpy as np
from sklearn.random_projection import SparseRandomProjection
X = np.random.rand(100, 10000)
sparseRandomProjection = SparseRandomProjection(
# -----------------------------------------------------
# Dimensionality of the target projection space.
# int
# 'auto'
n_components="auto",
# -----------------------------------------------------
# Ratio in the range (0, 1] of non-zero component in
# the random projection matrix.
# float
# 'auto'
density="auto",
# -----------------------------------------------------
# Semilla del generador de aleatorios
# None
# int
random_state=1234,
)
X_new = sparseRandomProjection.fit_transform(X)
X_new.shape
[4]:
(100, 3947)
https://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html
[5]:
from sklearn.datasets import load_digits
digits = load_digits(n_class=6, return_X_y=False)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
[6]:
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
ix = 10 * i + 1
for j in range(n_img_per_row):
iy = 10 * j + 1
img[ix : ix + 8, iy : iy + 8] = 1 - X[i * n_img_per_row + j].reshape((8, 8))
plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.show()

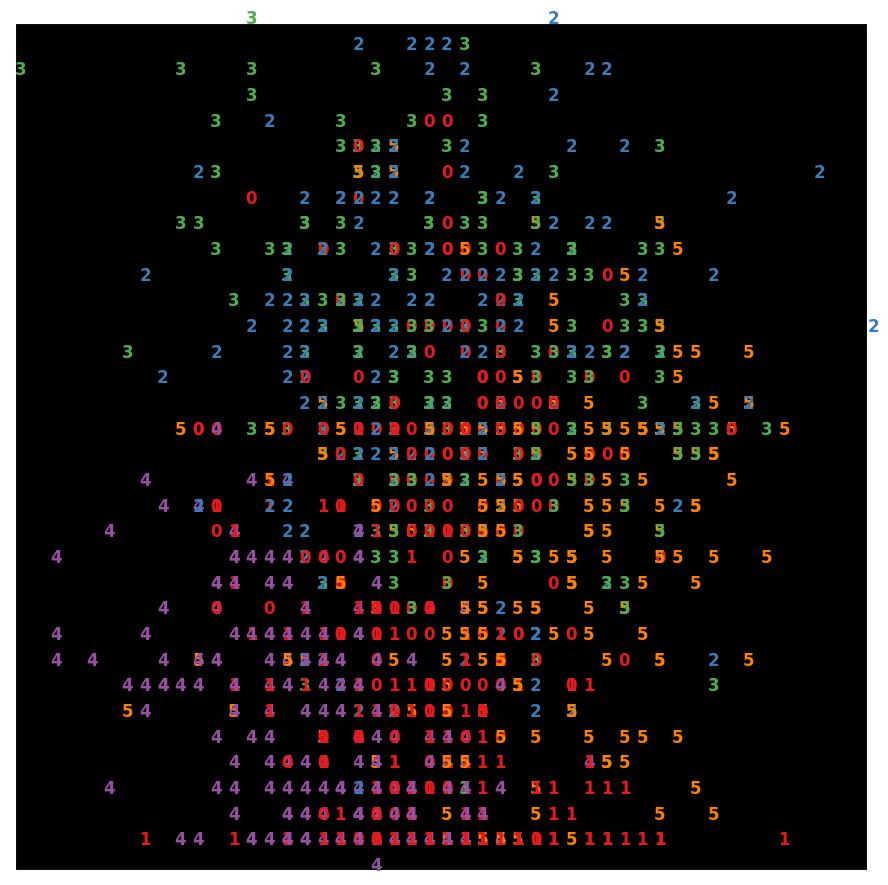
[7]:
sparseRandomProjection = SparseRandomProjection(
n_components=2,
random_state=42,
)
X_projected = sparseRandomProjection.fit_transform(X)
x_min, x_max = np.min(X_projected, 0), np.max(X_projected, 0)
X_scaled = (X_projected - x_min) / (x_max - x_min)
[8]:
from matplotlib import offsetbox
plt.figure(figsize=(11, 11))
plt.style.use("dark_background")
for i in range(X_scaled.shape[0]):
plt.text(
X_scaled[i, 0],
X_scaled[i, 1],
str(y[i]),
color=plt.cm.Set1(y[i] / 10.0),
fontdict={"weight": "bold", "size": 12},
)
plt.xticks([])
plt.yticks([])
plt.show()