MLPClassifier

• Ultima modificación: 2023-03-11 | YouTube

• En clasificación binaria, la función logística es usada la activación de la neurona de salida. Valores superiores a 0.5 indican pertenencia a la clase positiva, mientras que valores inferiores a 0.5 indican pertenencia a la clase negativa.

• Para clasificación con más de dos clases, se tiene una neurona de salida por cada clase, y el cálculo de la activación se hace mediante la función softmax:

  \text{softmax}(z)_i = \frac{\exp(z_i)}{\sum_i \exp(z_i)}

  donde z_i representa el i-ésimo elemento que corresponde a la clase i. El resultado es la probabilidad de pertenencia del patrón x a la clase i. El patrón se asigna a la clase con probabilidad más alta.

• En este caso, se minimiza el promedio de la función de entropia cruzada, que para el caso binario es: $$ \text{Loss}`(:nbsphinx-math:hat{y}`, y, W) = \frac{1}{n} \sum_{i=0}^n \left`( y_i :nbsphinx-math:log :nbsphinx-math:hat{y}`_i + (1 - y_i) \exp `(1 - :nbsphinx-math:hat{y}`_i) \right)

• \frac{\alpha}{2n} ||W||_2^2 $$

from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, shuffle=False)

from sklearn.neural_network import MLPClassifier

#
# NOTA: Usa los mismos parámetros que MLPRegressor
#
mlpClassifier = MLPClassifier(
    # --------------------------------------------------------------------------
    # The ith element represents the number of neurons in the ith hidden layer.
    hidden_layer_sizes=(6,),
    # --------------------------------------------------------------------------
    # Activation function for the hidden layer.
    # * ‘identity’
    # * 'logistic'
    # * 'tanh'
    # * 'relu'
    # activation='relu',
    activation="logistic",
    # --------------------------------------------------------------------------
    # The solver for weight optimization.
    # * 'lbfgs'
    # * 'sgd'
    # * 'adam'
    solver="adam",
    # --------------------------------------------------------------------------
    # Strength of the L2 regularization term.
    alpha=0.0001,
    # --------------------------------------------------------------------------
    # Size of minibatches for stochastic optimizers. If the solver is ‘lbfgs’,
    # the classifier will not use minibatch. When set to “auto”,
    # batch_size=min(200, n_samples).
    batch_size='auto',
    # --------------------------------------------------------------------------
    # Learning rate schedule for weight updates. Only used when solver=’sgd’.
    # * ‘constant’ is a constant learning rate given by ‘learning_rate_init’.
    # * ‘invscaling’ gradually decreases the learning rate learning_rate_ at
    #   each time step ‘t’ using an inverse scaling exponent of ‘power_t’.
    #   effective_learning_rate = learning_rate_init / pow(t, power_t)
    # * ‘adaptive’ keeps the learning rate constant to ‘learning_rate_init’ as
    #   long as training loss keeps decreasing. Each time two consecutive
    #   epochs fail to decrease training loss by at least tol, or fail to
    #   increase validation score by at least tol if ‘early_stopping’ is on,
    #   the current learning rate is divided by 5.
    learning_rate='constant',
    # --------------------------------------------------------------------------
    # The initial learning rate used. It controls the step-size in updating the
    # weights. Only used when solver=’sgd’ or ‘adam’.
    # learning_rate_init=0.001,
    learning_rate_init=0.1,
    # --------------------------------------------------------------------------
    # The exponent for inverse scaling learning rate. It is used in updating
    # effective learning rate when the learning_rate is set to ‘invscaling’.
    # Only used when solver=’sgd’.
    power_t=0.5,
    # --------------------------------------------------------------------------
    # Maximum number of iterations. The solver iterates until convergence
    # (determined by ‘tol’) or this number of iterations. For stochastic solvers
    # (‘sgd’, ‘adam’), note that this determines the number of epochs (how many
    # times each data point will be used), not the number of gradient steps.
    # default: 200
    max_iter=1000,
    # --------------------------------------------------------------------------
    # Whether to shuffle samples in each iteration. Only used when solver=’sgd’
    # or ‘adam’.
    shuffle=True,
    # --------------------------------------------------------------------------
    # Determines random number generation for weights and bias initialization,
    # train-test split if early stopping is used, and batch sampling when
    # solver=’sgd’ or ‘adam’.
    random_state=None,
    # --------------------------------------------------------------------------
    # Tolerance for the optimization. When the loss or score is not improving
    # by at least tol for n_iter_no_change consecutive iterations, unless
    # learning_rate is set to ‘adaptive’, convergence is considered to be
    # reached and training stops.
    tol=1e-4,
    # --------------------------------------------------------------------------
    # When set to True, reuse the solution of the previous call to fit as
    # initialization, otherwise, just erase the previous solution.
    warm_start=False,
    # --------------------------------------------------------------------------
    # Momentum for gradient descent update. Should be between 0 and 1. Only
    # used when solver=’sgd’.
    momentum=0.9,
    # --------------------------------------------------------------------------
    # Whether to use Nesterov’s momentum. Only used when solver=’sgd’ and
    # momentum > 0.
    nesterovs_momentum=True,
    # --------------------------------------------------------------------------
    # Whether to use early stopping to terminate training when validation score
    # is not improving. If set to true, it will automatically set aside 10% of
    # training data as validation and terminate training when validation score
    # is not improving by at least tol for n_iter_no_change consecutive epochs.
    # Only effective when solver=’sgd’ or ‘adam’.
    early_stopping=False,
    # --------------------------------------------------------------------------
    # The proportion of training data to set aside as validation set for early
    # stopping. Must be between 0 and 1. Only used if early_stopping is True.
    validation_fraction=0.1,
    # --------------------------------------------------------------------------
    # Exponential decay rate for estimates of first moment vector in adam,
    # should be in [0, 1). Only used when solver=’adam’.
    beta_1=0.9,
    # --------------------------------------------------------------------------
    # Exponential decay rate for estimates of second moment vector in adam,
    # should be in [0, 1). Only used when solver=’adam’.
    beta_2=0.999,
    # --------------------------------------------------------------------------
    # Value for numerical stability in adam. Only used when solver=’adam’.
    epsilon=1e-8,
    # --------------------------------------------------------------------------
    # Maximum number of epochs to not meet tol improvement. Only effective when
    # solver=’sgd’ or ‘adam’.
    n_iter_no_change=10,
    # --------------------------------------------------------------------------
    # Only used when solver=’lbfgs’. Maximum number of function calls. The
    # solver iterates until convergence (determined by ‘tol’), number of
    # iterations reaches max_iter, or this number of function calls.
    max_fun=15000,
)

import numpy as np

mlpClassifier.fit(X, y)

MLPClassifier(activation='logistic', hidden_layer_sizes=(6,),
              learning_rate_init=0.1, max_iter=1000)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

#
# Class labels for each output.
#
mlpClassifier.classes_

array([0, 1])

#
# The current loss computed with the loss function.
#
mlpClassifier.loss_

0.010162214219101302

#
# The minimum loss reached by the solver throughout fitting.
#
mlpClassifier.best_loss_

0.010162214219101302

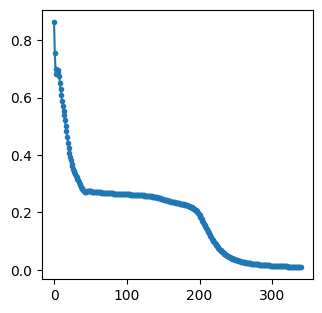
import matplotlib.pyplot as plt

#
# Loss value evaluated at the end of each training step. The ith element in the
# list represents the loss at the ith iteration.
#
plt.figure(figsize=(3.5, 3.5))
plt.plot(mlpClassifier.loss_curve_, ".-")
plt.show()

#
# The ith element in the list represents the weight matrix corresponding to
# layer i.
#
mlpClassifier.coefs_

[array([[-9.83226894,  1.76538747, -4.22179774,  6.85910764, -9.44908223,
          0.32718328],
        [-6.69983696, -8.79329737,  3.69923602, -3.60274196,  5.46374771,
         -5.65077695]]),
 array([[ 8.2538032 ],
        [ 2.66797414],
        [-5.86564647],
        [ 4.71004377],
        [-7.82510337],
        [ 2.66264125]])]

#
# The ith element in the list represents the bias vector corresponding to layer
# i + 1.
#
mlpClassifier.intercepts_

[array([ 6.47236782,  5.62647735,  5.86524544, -9.46880502, -5.86346682,
        -1.71942688]),
 array([-1.2678123])]

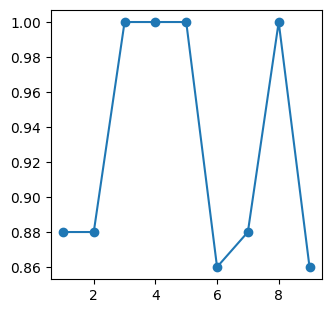
score = []

for h in range(1, 10):

    mlpClassifier = MLPClassifier(
        hidden_layer_sizes=(h,),
        activation="logistic",
        solver="adam",
        alpha=0.0,
        learning_rate='constant',
        learning_rate_init=0.1,
        max_iter=1000,
        random_state=1,
    )

    mlpClassifier.fit(X, y)
    score.append(mlpClassifier.score(X, y))

plt.figure(figsize=(3.5, 3.5))
plt.plot(range(1, 10), score, "-o")

[<matplotlib.lines.Line2D at 0x7fca2c959fa0>]