Restricted Boltzmann machines — 10:25 min

• 10:25 min | Última modificación: Septiembre 22, 2021 | YouTube

Este es un modelo de aprendizaje no supervizado (red neuronal) que permite capturar las relaciones probabilisticas entre los datos.

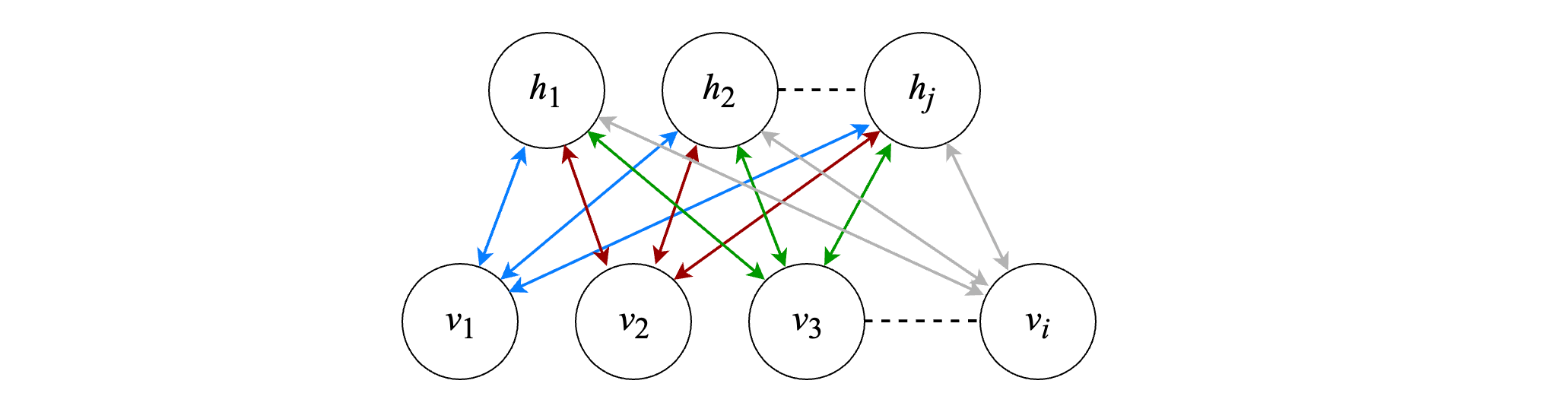
• Su arquitectura esta compuesta por dos capas: una visible (con nodos v_i) y una oculta (con nodos h_j).

• Las entradas y las salidas son binarias {0, 1}.

• La señal se propaga de la capa de entrada a la capa oculta como:

P(h_j = 1 | \mathbf{v}) = \sigma \left( \sum_i w_{ij} \; v_i + c_j \right)

• Luego, la señal de salida de la capa oculta se propaga a la capa de entrada como:

P(v_i = 1 | \mathbf{h}) = \sigma \left( \sum_j w_{ij} \; h_j + b_i \right)

• El modelo usa la función logistica para la activación de las neuronas:

\sigma(u) = \frac{1}{1 + \exp(-u)}

Esta red neuronal funciona como un autoencoder, donde la red apende a reproducir su salida.

La función de energía de la red esta dada como:

E(\mathbf{v}, \mathbf{h}) = - \sum_i \sum_j w_{ij} v_i h_j - \sum_i b_i v_i - \sum_j c_j h_j

El térnino restringido se refiere a que está prohibida la intercación directa entre neuronas de la misma capa.

En el siguiente ejemplo, esta red neuroal es usada para extraer las características no lineales de los datos.

import numpy as np
from sklearn.datasets import load_digits

digits = load_digits(n_class=6, return_X_y=False)
X = digits.data
y = digits.target

from scipy.ndimage import convolve


def nudge_dataset(X, Y):

    direction_vectors = [
        [[0, 1, 0], [0, 0, 0], [0, 0, 0]],
        [[0, 0, 0], [1, 0, 0], [0, 0, 0]],
        [[0, 0, 0], [0, 0, 1], [0, 0, 0]],
        [[0, 0, 0], [0, 0, 0], [0, 1, 0]],
    ]

    def shift(x, w):
        return convolve(x.reshape((8, 8)), mode="constant", weights=w).ravel()

    X = np.concatenate(
        [X] + [np.apply_along_axis(shift, 1, X, vector) for vector in direction_vectors]
    )
    Y = np.concatenate([Y for _ in range(5)], axis=0)
    return X, Y


X = np.asarray(X, "float32")
X, Y = nudge_dataset(X, y)

from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neural_network import BernoulliRBM
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import minmax_scale

X = minmax_scale(X, feature_range=(0, 1))

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)


rbm = Pipeline(
    steps=[
        (
            "rbm",
            BernoulliRBM(
                random_state=0,
                learning_rate=0.06,
                n_iter=10,
                n_components=100,
            ),
        ),
        (
            "logistic",
            LogisticRegressionCV(
                Cs=20,
                solver="newton-cg",
                tol=1,
            ),
        ),
    ]
)

rbm.fit(X_train, Y_train)


display(
    accuracy_score(Y_train, rbm.predict(X_train)),
    accuracy_score(Y_test, rbm.predict(X_test)),
)

0.9824561403508771

0.9732225300092336

from sklearn.linear_model import LogisticRegressionCV

logisticRegressionCV = LogisticRegressionCV(
    solver="newton-cg",
    tol=1,
)

logisticRegressionCV.fit(X_train, Y_train)

display(
    accuracy_score(Y_train, logisticRegressionCV.predict(X_train)),
    accuracy_score(Y_test, logisticRegressionCV.predict(X_test)),
)

0.8845798707294552

0.8559556786703602