Algoritmo de agrupamiento K-means#
Este es el problema inverso al de clasificación. En la siguiente figura se desea determinar cuántos grupos existen en un conjunto de datos y los centroides de dichos grupos, tal que los miembros de cada grupo tengan unas características similares. El centroide de cada grupo representa a los miembros de su grupo.
[1]:
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
X, y = make_blobs(
n_samples=90,
n_features=2,
centers=[
[8, -8],
[7, 8],
[-6, -1],
],
cluster_std=2.0,
shuffle=False,
random_state=5,
)
plt.figure(figsize=(4, 4))
plt.scatter(
X[:, 0],
X[:, 1],
color="tab:gray",
edgecolors="k",
s=50,
alpha=0.9,
)
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.axis("equal")
plt.show()
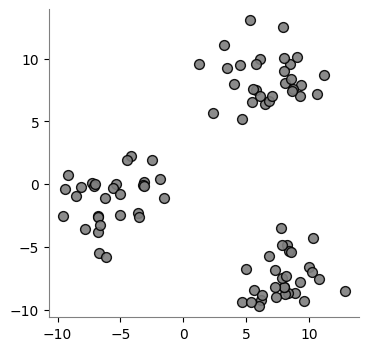
En el algoritmo K-means, se pretende minimizar la distancia entre los miembros de cada grupo y maximizar la distancia entre grupos, también conocido como principio de inercia. Para ello, en este algoritmo se minimiza:
\sum_{i=1}^k \sum_{\mathbf{x}_j \in S_i} \text{dist}( \mathbf{x}_j, \mathbf{u}_i)
Si se usa la norma euclidiana:
\text{dist}( \mathbf{x}_j, \mathbf{u}_i) = \| \mathbf{x}_j - \mathbf{u}_i \|^2 = \sum_{p=1}^P (x_{jp} - u_{ip})^2
La inercia es reconocida como una medida de la coherencia interna de los patrones que representan cada cluster o grupo.
Se sabe que esta métrica sufre varios problemas:
Asume que los clusters son convexos e isotropicos, por lo que tiene una efectividad limitada para clusters elogados o con formas irregulares.
La inercia es un valor no normalizado, por que se sabe que los valores bajos son mejores y que un valor de cero es óptimo.
Las distancias euclidianas en altas dimensiones tienden a ser infladas, por lo que las técnicas para reducir la dimensionalidad son consideradas para el preprocesamiento de los datos.
Este proceso se realiza en dos fases:
Paso 1: Se generan los centros iniciales \mathbf{u}_i. Podrían ser aleatorios o seleccionados entre los datos.
[2]:
#
# Se generan tres centros elatorios iniciales
#
import numpy as np
centers = np.array(
[
[-5, 7],
[0, -8],
[13, 0],
],
dtype=np.float64,
)
Paso 2: Dados los centros de los clusters \mathbf{u}_i, se calcula la distancia de cada uno de los puntos del dataset a los centros de los clusters.
[3]:
from sklearn.metrics.pairwise import euclidean_distances
distances = euclidean_distances(X, centers)
distances[:5, :]
[3]:
array([[20.92875212, 8.9070706 , 9.59061636],
[23.65194338, 12.87142082, 8.50531131],
[17.74305182, 8.80752849, 6.79951841],
[19.67041089, 6.29376779, 11.4378307 ],
[20.59426138, 8.4011511 , 9.81732198]])
Paso 3: Se asigna cada punto del dataset al cluster más cercano.
[4]:
labels = np.argmin(distances, axis=1)
labels
[4]:
array([1, 2, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 1, 1,
2, 2, 1, 2, 1, 1, 2, 2, 0, 2, 2, 2, 0, 0, 2, 2, 2, 2, 2, 2, 2, 0,
2, 2, 2, 0, 2, 2, 2, 0, 2, 0, 0, 2, 2, 0, 2, 0, 0, 1, 0, 1, 0, 1,
1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0,
1, 1])
[5]:
from matplotlib.patches import Circle
def plot_clusters(X, centers, labels):
colors = ["tab:red", "tab:green", "tab:blue"]
plt.figure(figsize=(4, 4))
for cluster in np.unique(labels):
X_cluster = X[labels == cluster, :]
plt.scatter(
X_cluster[:, 0],
X_cluster[:, 1],
color=colors[cluster],
edgecolors="k",
s=50,
alpha=0.9,
)
for i in range(X_cluster.shape[0]):
plt.plot(
[centers[cluster, 0], X_cluster[i, 0]],
[centers[cluster, 1], X_cluster[i, 1]],
color=colors[cluster],
alpha=0.4,
)
plt.scatter(
centers[cluster, 0],
centers[cluster, 1],
marker="s",
color=colors[cluster],
edgecolors="k",
s=50,
alpha=0.9,
)
distances = euclidean_distances(
X_cluster, np.expand_dims(centers[cluster, :], axis=0)
).reshape(-1)
radius = distances.max()
plt.gca().add_patch(
Circle(
xy=centers[cluster, :],
radius=radius,
fill=False,
ec=colors[cluster],
ls="--",
)
)
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.axis("square")
plt.show()
plot_clusters(X, centers, labels)
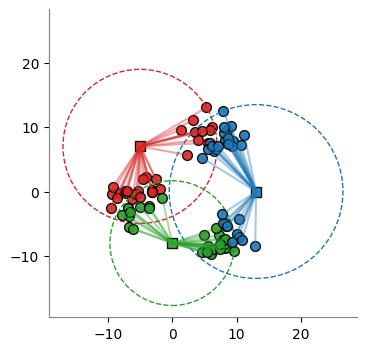
Paso 4: Se recalcula cada centro \mathbf{u}_i como el promedio de los puntos \mathbf{x}_j que pertenecen a él; es decir, la componente u_{ip} del centroide i es el promedio de las componentes x_{jp}.
[6]:
def compute_centers(X, centers, labels):
for cluster in np.unique(labels):
centers[cluster, :] = np.mean(
X[labels == cluster, :],
axis=0,
)
return centers
centers = compute_centers(X, centers, labels)
centers
[6]:
array([[-2.38591678, 3.2492107 ],
[ 2.45751494, -6.44235461],
[ 8.47942768, 3.03165143]])
El algoritmo se detiene cuando ningún punto cambia de cluster.
[7]:
#
# Iteración #2
#
distances = euclidean_distances(X, centers)
labels = np.argmin(distances, axis=1)
plot_clusters(X, centers, labels)
centers = compute_centers(X, centers, labels)
centers
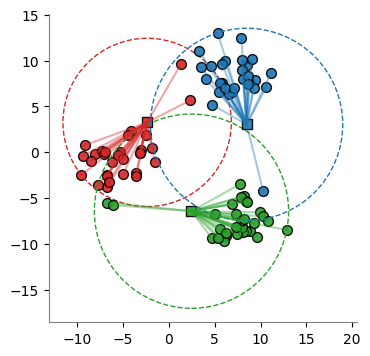
[7]:
array([[-5.19206228, -0.26197605],
[ 6.97409343, -7.43261021],
[ 7.13658938, 8.0416505 ]])
[8]:
#
# Iteración #3
#
distances = euclidean_distances(X, centers)
labels = np.argmin(distances, axis=1)
plot_clusters(X, centers, labels)
centers = compute_centers(X, centers, labels)
centers
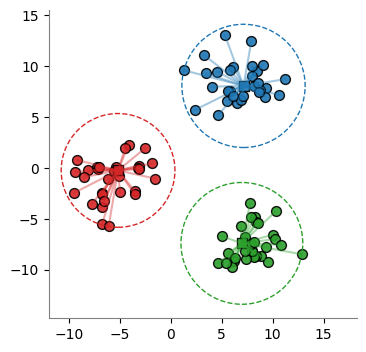
[8]:
array([[-5.7408924 , -1.1458363 ],
[ 7.97850671, -7.44748742],
[ 6.67558968, 8.42457928]])
[9]:
#
# Iteración #4
#
distances = euclidean_distances(X, centers)
labels = np.argmin(distances, axis=1)
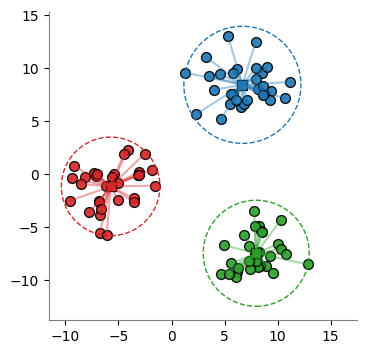
plot_clusters(X, centers, labels)
centers = compute_centers(X, centers, labels)
centers
[9]:
array([[-5.7408924 , -1.1458363 ],
[ 7.97850671, -7.44748742],
[ 6.67558968, 8.42457928]])
Agrupamiento usando KMeans en Python#
[10]:
from sklearn.cluster import KMeans
kmeans = KMeans(
# -------------------------------------------------------------------------
# Numero de clusters
n_clusters=3,
# -------------------------------------------------------------------------
# Algoritmo para inicializar los clusters:
# 'k-means++': Selecciona los puntos iniciales entre los datos del dataset
# 'random': aleatorio
init="k-means++",
# -------------------------------------------------------------------------
#
n_init=10,
# -------------------------------------------------------------------------
#
max_iter=300,
# -------------------------------------------------------------------------
#
random_state=None,
# -------------------------------------------------------------------------
# 'full': algoritmo clásico,
# 'elkan': variación con eficiencia computacional que evita computar las
# distancias entre todos los puntos.
algorithm="lloyd",
)
kmeans.fit(X)
kmeans.predict(X)
[10]:
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0], dtype=int32)
[11]:
#
# Centros de los clusters
#
kmeans.cluster_centers_
[11]:
array([[-5.7408924 , -1.1458363 ],
[ 7.97850671, -7.44748742],
[ 6.67558968, 8.42457928]])
[12]:
#
# Cluster asignado a cada punto
#
kmeans.labels_
[12]:
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0], dtype=int32)
[13]:
#
# Sum of squared distances of samples to their closest cluster center, weighted
# by the sample weights if provided.
#
kmeans.inertia_
[13]:
715.9389324313938
[14]:
kmeans.n_iter_
[14]:
2