Ridge Regression#
Este modelo impone una penalización al tamaño de los coeficientes.
Los coeficientes del modelo minimizan la suma penalizada de residuales al cuadrado:
\min_w ||Xw -y||_2^2 + \alpha ||w||_2^2
con \alpha \ge 0
La penalización se aplica únicamente sobre los coeficientes de x.
[1]:
from sklearn.datasets import make_regression
X, y_true = make_regression(
n_samples=100,
n_features=1,
n_informative=1,
bias=100.0,
tail_strength=0.9,
noise=12.0,
shuffle=False,
coef=False,
random_state=0,
)
[2]:
from sklearn.linear_model import Ridge
def predict(X, y_true, line_X, alpha):
ridge = Ridge(
# ---------------------------------------------------------------------
# Constant that multiplies the L2 term, controlling regularization
# strength. alpha must be a non-negative float. When alpha = 0, the
# objective is equivalent to ordinary least squares, solved by the
# LinearRegression object.
#
alpha=alpha,
# ---------------------------------------------------------------------
# Whether to fit the intercept for this model.
fit_intercept=True,
# ---------------------------------------------------------------------
# Maximum number of iterations for conjugate gradient solver.
max_iter=None,
# ---------------------------------------------------------------------
# Precision of the solution. Note that tol has no effect for solvers
# ‘svd’ and ‘cholesky’.
tol=1e-4,
# ---------------------------------------------------------------------
# Solver to use in the computational routines:
# * ‘auto’ chooses the solver automatically based on the type of data.
# * 'svd'
# * 'cholesky'
# * 'sparse_cg'
# * 'lsqr': regularized least-square
# * 'sag': Stochastic Average Gradient
# * 'lbfgs'
solver="auto",
# ---------------------------------------------------------------------
# When set to True, forces the coefficients to be positive.
positive=False,
# ---------------------------------------------------------------------
# Used when solver == ‘sag’ or ‘saga’ to shuffle the data.
random_state=None,
)
ridge.fit(X, y_true)
y_predicted = ridge.predict(line_X)
# Main attributes:
print(ridge.coef_)
print(ridge.intercept_)
return y_predicted
[3]:
import matplotlib.pyplot as plt
import numpy as np
def plot(X, y_true, alpha):
line_X = np.linspace(X.min(), X.max())[:, np.newaxis]
plt.figure(figsize=(3.5, 3.5))
plt.scatter(X, y_true, color="tab:blue", alpha=0.8, edgecolors="white")
plt.plot(line_X, predict(X, y_true, line_X, alpha), "k", linewidth=2)
plt.title("alpha =" + str(alpha))
[4]:
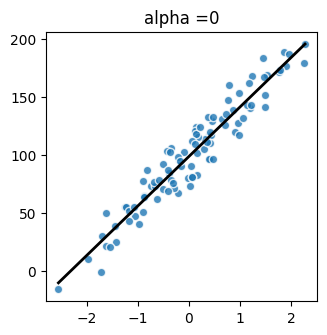
plot(X, y_true, 0)
[42.66621538]
99.02298180756313
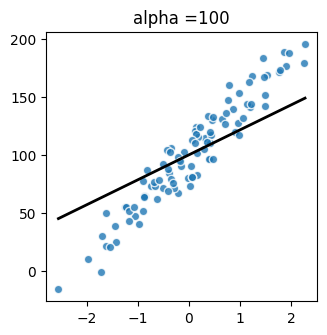
[5]:
plot(X, y_true, 100)
[21.50059777]
100.28885539402634
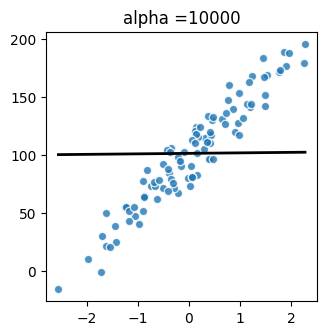
[6]:
plot(X, y_true, 10000)
[0.42905631]
101.54910247355808