Modelo del perceptrones multicapa

• Ultima modificación: 2023-03-11 | YouTube

• Es un modelo matemático basado en la representación de las redes de neuronas biológicas.

• Dado un conjunto de características X=x_1, x_2, \ldots, x_m y una variable dependiente y, el modelo puede aprender la relación no lineal y deterministica entre ellas.

• El siguiente diagrama representa un perceptrón multicapa con una capa de entreada, una capa oculta y una de salida.

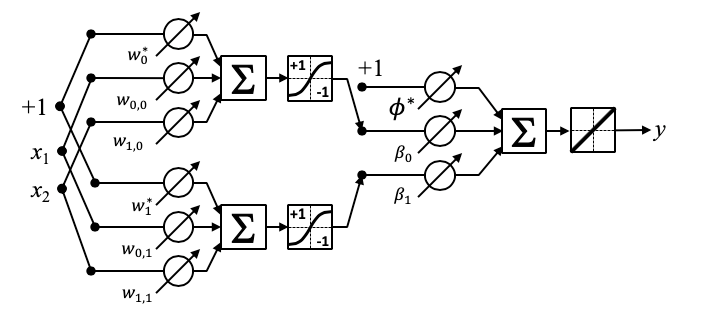
• Cada neurona de la capa oculta transforma los valores de la capa previa con una suma ponderada w_0 + w_1 x_1 + \ldots + w_m x_m, seguida de una función de activación no lineal g(\cdot): R \rightarrow R

• La capa de salida transforma los valores de la capa oculta usando el mismo modelo matemático de la capa oculta, y usando como función de activación g(u)=u.

• Propagación de una señal a través del modelo: Sea un MLP con 2 entradas y 3 neuronas en la capa oculta.

import numpy as np

# Entrada al MLP
x = np.array([1, 2])

# Matriz de pesos de la capa de entrada a la capa oculta
Wih = np.array(
    [
        [0.1, 0.2, 0.3],
        [0.4, 0.5, 0.6],
    ]
)

# vector de pesos de las neuronas bias
Wh = np.array([0.6, 0.7, 0.8])

# Entrada a la capa oculta:
#   1 * 0.1 + 2 * 0.4 + 0.6 = 1.5
#   1 * 0.2 + 2 * 0.5 + 0.7 = 1.9
#   1 * 0.3 + 2 * 0.6 + 0.8 = 2.3
input_hidden_layer = np.matmul(x, Wih) + Wh
input_hidden_layer

array([1.5, 1.9, 2.3])

# Salida de la capa oculta:
#   tanh(1.5) = 0.9051
#   tanh(1.9) = 0.9562
#   tanh(2.3) = 0.9800
output_hidden_layer = np.tanh(input_hidden_layer)
output_hidden_layer

array([0.90514825, 0.95623746, 0.9800964 ])

# matriz de pesos de la capa oculta a la capa de salida
Who = np.array([[-1], [0], [1]])

# Peso de la neurona bias de la capa de salida
Wo = 1

# Salida de la capa oculta (recuerde que g(u) = u):
# 1 - 1 * 0.9051 + 0 * 0.9562 + 1 * 0.9800 = 1.0749
np.matmul(output_hidden_layer, Who) + Wo

array([1.07494814])