Perceptrón simple#
El problema de clasificación binaria (con clases C_1 y C_2 dicotómicas) se define de la siguiente manera:
Cada patrón de entrada tiene la forma \mathbf{x}=[+1,x_1,x_2,…,x_n ].
Las clases C_1 y C_2 se representan como \{-1, +1\} respectivamente.
Los parámetros del perceptrón binario son \mathbf{w}=[w_0,w_1,…,w_n] tal que y=\varphi(\mathbf{w}^T \mathbf{x}), donde \varphi(.) es un conmutador bipolar.
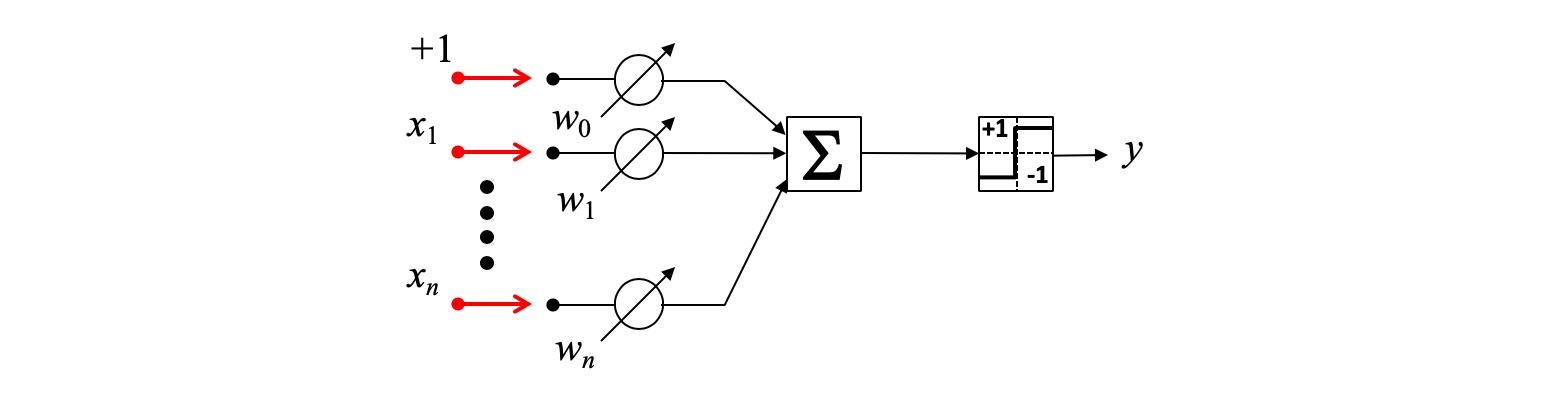
Note que \mathbf{w}^T \mathbf{x} es un modelo lineal.
Se desea encontrar el vector \mathbf{w} tal que el perceptrón clasifique correctamente todos los patrones de entrenamiento.
La función de pérdida del perceptrón se basa en el cálculo del error e_k definido como:
e_k= d_k-y_k = d_k - \varphi(\mathbf{w}^T_k \mathbf{x}_k) = \begin{cases} 0, & \text{Si $d_k = y_k$}\\ +2, & \text{Si $d_k = +1$ y $y_k = -1$}\\ -2, & \text{Si $d_k = -1$ y $y_k = +1$}\\ \end{cases}
Los parámetros del modelo son estimados numéricamente usando el método del gradiente descendente:
\mathbf{w}_{k+1} = \mathbf{w}_k+e_k \mathbf{x}_k
El perceptrón es equivalente a:
SGDClassifier(loss="perceptron", eta0=1, learning_rate="constant", penalty=None).
[1]:
from sklearn.datasets import load_breast_cancer
X, y = load_breast_cancer(return_X_y=True)
[2]:
from sklearn.linear_model import Perceptron
perceptron = Perceptron(
# --------------------------------------------------------------------------
# Specify the norm of the penalty:
# * None: no penalty is added.
# * 'l2': add a L2 penalty term and it is the default choice.
# * 'l1': add a L1 penalty term.
# * 'elasticnet': both L1 and L2 penalty terms are added.
penalty=None,
# --------------------------------------------------------------------------
# Constant that multiplies the regularization term if regularization is
# used.
alpha=0.0001,
# --------------------------------------------------------------------------
# The Elastic Net mixing parameter, with 0 <= l1_ratio <= 1. l1_ratio=0
# corresponds to L2 penalty, l1_ratio=1 to L1. Only used if
# penalty='elasticnet'.
l1_ratio=0.15,
# --------------------------------------------------------------------------
# Whether the intercept should be estimated or not. If False, the data is
# assumed to be already centered.
fit_intercept=True,
# --------------------------------------------------------------------------
# The maximum number of passes over the training data (aka epochs). It only
# impacts the behavior in the fit method, and not the partial_fit method.
max_iter=1000,
# --------------------------------------------------------------------------
# The stopping criterion. If it is not None, the iterations will stop when
# (loss > previous_loss - tol).
tol=1e-3,
# --------------------------------------------------------------------------
# Whether or not the training data should be shuffled after each epoch.
shuffle=True,
# --------------------------------------------------------------------------
# Constant by which the updates are multiplied.
eta0=1,
# --------------------------------------------------------------------------
# Used to shuffle the training data, when shuffle is set to True. Pass an
# int for reproducible output across multiple function calls.
random_state=0,
# --------------------------------------------------------------------------
# Whether to use early stopping to terminate training when validation. score
# is not improving. If set to True, it will automatically set aside a
# stratified fraction of training data as validation and terminate training
# when validation score is not improving by at least tol for
# n_iter_no_change consecutive epochs.
early_stopping=False,
# --------------------------------------------------------------------------
# The proportion of training data to set aside as validation set for early
# stopping. Must be between 0 and 1. Only used if early_stopping is True.
validation_fraction=0.1,
# --------------------------------------------------------------------------
# Number of iterations with no improvement to wait before early stopping.
n_iter_no_change=5,
# --------------------------------------------------------------------------
# Weights associated with classes. If not given, all classes are supposed to
# have weight one. The “balanced” mode uses the values of y to automatically
# adjust weights inversely proportional to class frequencies in the input
# data as n_samples / (n_classes * np.bincount(y)).
class_weight=None,
# --------------------------------------------------------------------------
# When set to True, reuse the solution of the previous call to fit as
# initialization, otherwise, just erase the previous solution.
warm_start=False,
)
perceptron.fit(X, y)
perceptron.predict(X)
[2]:
array([0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0,
1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0,
1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0,
1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1,
1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0,
0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1,
1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1,
1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1,
0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1,
1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0,
1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1,
1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1,
1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1])
[3]:
perceptron.score(X, y)
[3]:
0.9261862917398945
[4]:
perceptron.intercept_
[4]:
array([301.])
[5]:
perceptron.coef_
[5]:
array([[ 2.30434100e+03, 2.97808000e+03, 1.32373800e+04,
4.55750000e+03, 1.99728200e+01, -1.39147700e+01,
-4.75552493e+01, -1.99746190e+01, 3.85718000e+01,
1.62372600e+01, 6.11430000e+00, 2.13245700e+02,
-1.26940700e+02, -6.19829200e+03, 9.33463000e-01,
-3.70119900e+00, -6.05731830e+00, -8.79828000e-01,
3.13196800e+00, 1.54238900e-01, 2.42195700e+03,
3.69363000e+03, 1.31086400e+04, -6.70030000e+03,
2.39875500e+01, -5.68726600e+01, -1.05821866e+02,
-2.51252590e+01, 4.93057000e+01, 1.36139600e+01]])