Regresión de Huber (HuberRegressor)

• Regresión lineal con regularización L2 que es robusta a outliers.

• Difiere de Ridge porque aplica una pérdida lineal a los puntos que son clasificados como outliers.

• No ignora el efecto de los outliers pero si lo minimiza.

import numpy as np
from sklearn.datasets import make_regression

#
# Generación de datos
#
rng = np.random.RandomState(0)
X, y = make_regression(
    n_samples=20,
    n_features=1,
    random_state=0,
    noise=4.0,
    bias=100.0,
)

X, y

(array([[-0.15135721],
        [ 0.40015721],
        [ 0.97873798],
        [-0.85409574],
        [-0.97727788],
        [ 0.3130677 ],
        [-0.10321885],
        [-0.20515826],
        [ 0.33367433],
        [ 1.49407907],
        [ 0.95008842],
        [ 0.12167502],
        [ 1.45427351],
        [ 1.86755799],
        [ 0.14404357],
        [ 0.4105985 ],
        [ 0.76103773],
        [ 2.2408932 ],
        [ 0.44386323],
        [ 1.76405235]]),
 array([ 98.01970393, 108.45865411, 107.77654399,  90.31520078,
         92.04796546, 100.14472604, 104.37128562,  95.20896669,
        102.50526212, 122.11966081, 112.28760019, 107.32614044,
        121.44454917, 125.80345967, 104.3306721 , 112.02618102,
        106.59661396, 129.8571502 , 113.51286154, 125.42202601]))

#
# Adiciona cuatro outliers fuertes al dataset
#
X_outliers = rng.normal(0, 0.5, size=(4, 1))
y_outliers = rng.normal(0, 2.0, size=4)

X_outliers[:2, :] += X.max() + X.mean() / 4.0
X_outliers[2:, :] += X.min() - X.mean() / 4.0

y_outliers[:2] += y.min() - y.mean() / 4.0
y_outliers[2:] += y.max() + y.mean() / 4.0

X = np.vstack((X, X_outliers))
y = np.concatenate((y, y_outliers))

from sklearn.linear_model import HuberRegressor

huberRegressor = HuberRegressor(
    # -------------------------------------------------------------------------
    # The parameter epsilon controls the number of samples that should be
    # classified as outliers. The smaller the epsilon, the more robust it is to
    # outliers.
    epsilon=1.35,
    # -------------------------------------------------------------------------
    # Maximum number of iterations that
    # scipy.optimize.minimize(method="L-BFGS-B") should run for.
    max_iter=100,
    # -------------------------------------------------------------------------
    # Strength of the squared L2 regularization. Note that the penalty is equal
    # to alpha * ||w||^2.
    alpha=0.0001,
    # -------------------------------------------------------------------------
    # Whether or not to fit the intercept. This can be set to False if the data
    # is already centered around the origin.
    fit_intercept=True,
)

huberRegressor.fit(X, y)

HuberRegressor()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

from sklearn.linear_model import Ridge

ridge = Ridge(
    fit_intercept=True,
    alpha=0.0,
    random_state=0,
)

ridge.fit(X, y)

Ridge(alpha=0.0, random_state=0)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

import matplotlib.pyplot as plt

plt.figure(figsize=(12, 5))
plt.plot(X, y, "b.")

x = np.linspace(X.min(), X.max(), 7).reshape(-1,1)

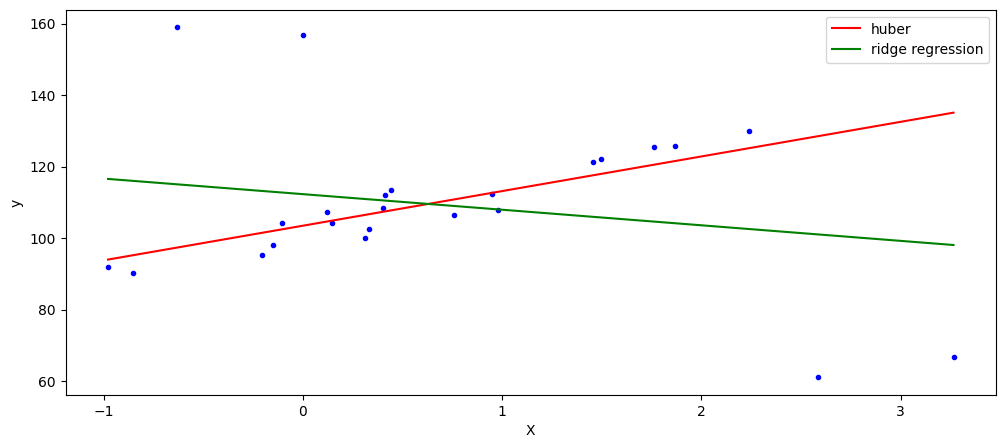
plt.plot(x, huberRegressor.predict(x), 'r-', label="huber")
plt.plot(x, ridge.predict(x), "g-", label="ridge regression")
plt.xlabel("X")
plt.ylabel("y")
plt.legend(loc=0)
plt.show()