SVC (Support Vector Classifier)#
### Función de riesgo
La estimación de los parámetros del modelo y la correspondiente selección de los vectores de soporte se realiza mediante la minimización de la función de riesgo regularizado de la forma:
R(C, \epsilon) = C \sum_i \text{loss}(d_i, y_i) + \sum_d w_d^2
La función de pérdida utilizada depende del tipo de implementación.
El término
K(x_i, x_j) = \phi(x_i)^T \phi(x_j)
donde \phi(\cdot) es una función kernel, y el término anterior corresponde al Kernel Trick.
Estimación de parámetros#
Sea un conjunto de patrones de entrenamiento \mathbf{x}_i \in \mathbb{R}^p, i=1, \dots, n, y y_i la variable dependiente con y \in \{-1, +1 \}, el objetivo es encontrar w \in \mathbb{R}^p y b \in \mathbb{R}, tal que la ecuación anterior sea correcta para la mayor cantidad de patrones.
Para la clasificación, esto equivale a resolver el problema primal:
\min_{w,b, \zeta} \;\;\; \frac{1}{2} w^T w \; + \; C \sum_{i=1}^n \zeta_i
sujeto a:
\begin{split} y_i \left( w^T \phi(x_i)+ b \right) \ge \; & 1 - \zeta_i \\ \\ \zeta_i \ge & \; 0 \\ \\ i= & 1, ..., n \\ \end{split}
Una explicación intuitiva es la siguiente:
Para llegar al óptimo se debe minimizar 0.5 w^Tw, es decir, se desean llevar los coeficientes a cero.
w^T \phi(x_i)+ b es la frontera de decisión entre las clases
Si un patrón es correctamente clasificado, entonces \zeta = 0.
Si un patrón es mal clasificado, \zeta > 0 haciendo crecer el segundo término de la función objetivo.
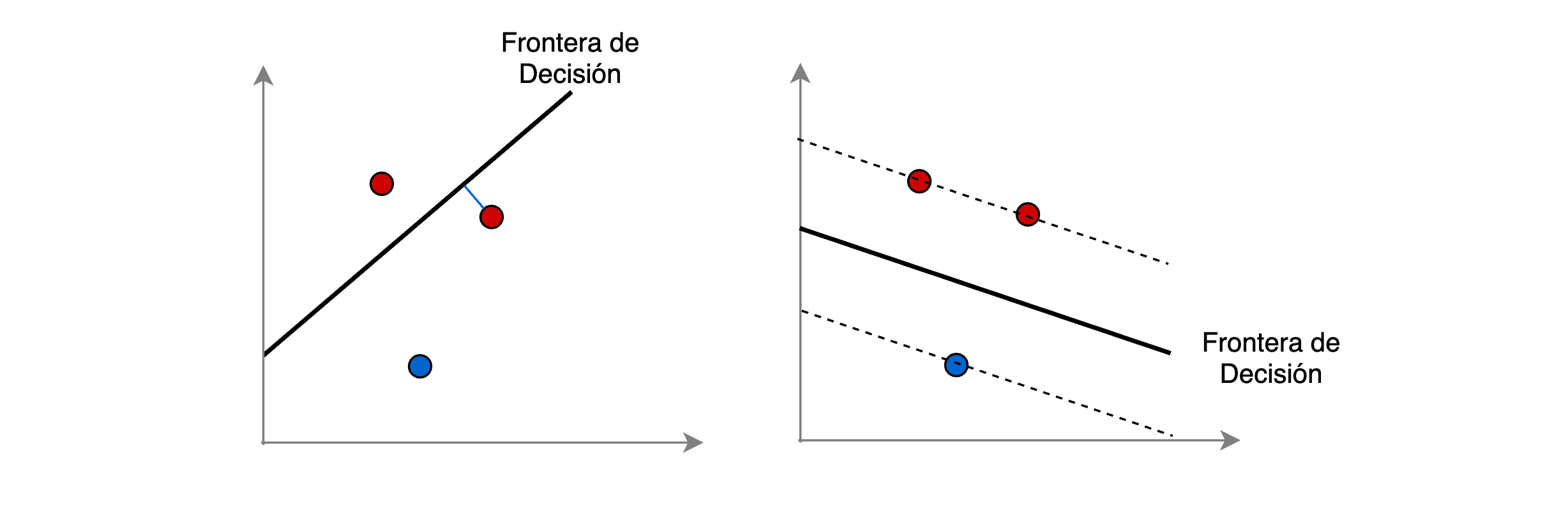
El parámetro C controla la fuerza de la penalización, y como resultado, actua como el inverso de un parámetro de regularización.
Problema dual#
El problema dual del primal es:
\min_\alpha \frac{1}{2} \alpha^T Q \alpha - e^T \alpha
sujeto a:
y^T\alpha = 0
0 \le \alpha_i \le C, \qquad i=1,\dots n
donde:
e es un vector de unos.
Q es una matriz semidefinida positiva de n \times n.
Q_{ij} = y_i y_j K(x_i, x_j)
K(x_i, x_j) = \phi(x_i)^T \phi(x_j)
\alpha_i son los coeficientes duales
### Frontera de decisión
Una vez el problema de optimización ha sido resuelto, la función de decisión se computa para una muestra x como:
\sum_{i \text{ in } SV} y_i \alpha_i K(x_i, x) + b
[1]:
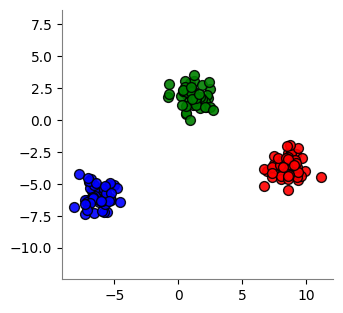
from sklearn.datasets import make_blobs
NPOINTS = 150
X, d = make_blobs(
n_samples=NPOINTS,
n_features=2,
centers=3,
cluster_std=0.8,
shuffle=False,
random_state=12345,
)
[2]:
import matplotlib.pyplot as plt
plt.figure(figsize=(3.5, 3.5))
plt.scatter(X[:50, 0], X[:50, 1], color="red", edgecolors="black", alpha=0.9, s=50)
plt.scatter(
X[50:100, 0], X[50:100, 1], color="blue", edgecolors="black", alpha=0.9, s=50
)
plt.scatter(X[100:, 0], X[100:, 1], color="green", edgecolors="black", alpha=0.9, s=50)
plt.gca().spines["left"].set_color("gray")
plt.gca().spines["bottom"].set_color("gray")
plt.gca().spines["top"].set_visible(False)
plt.gca().spines["right"].set_visible(False)
plt.axis("equal")
plt.show()
[3]:
from sklearn.svm import SVC
svc = SVC(
# --------------------------------------------------------------------------
# Regularization parameter. The strength of the regularization is inversely
# proportional to C. Must be strictly positive. The penalty is a squared l2
# penalty.
C=1,
# --------------------------------------------------------------------------
# Specifies the kernel type to be used in the algorithm. If none is given,
# ‘rbf’ will be used.
kernel="linear",
# --------------------------------------------------------------------------
# Degree of the polynomial kernel function (‘poly’). Must be non-negative.
# Ignored by all other kernels.
degree=3,
# --------------------------------------------------------------------------
# Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
# * if gamma='scale' (default) is passed then it uses
# 1 / (n_features * X.var()) as value of gamma,
# * if ‘auto’, uses 1 / n_features
# * if float, must be non-negative.
gamma="scale",
# --------------------------------------------------------------------------
# Independent term in kernel function. It is only significant in ‘poly’ and
# ‘sigmoid’.
coef0=0.0,
# --------------------------------------------------------------------------
# Whether to enable probability estimates. This must be enabled prior to
# calling fit, will slow down that method as it internally uses 5-fold
# cross-validation, and predict_proba may be inconsistent with predict.
probability=False,
# --------------------------------------------------------------------------
# Tolerance for stopping criterion.
tol=1e-3,
# --------------------------------------------------------------------------
# Set the parameter C of class i to class_weight[i]*C for SVC. If not
# given, all classes are supposed to have weight one. The “balanced” mode
# uses the values of y to automatically adjust weights inversely
# proportional to class frequencies in the input data as
# n_samples / (n_classes * np.bincount(y)).
class_weight=None,
# --------------------------------------------------------------------------
# Hard limit on iterations within solver, or -1 for no limit.
max_iter=-1,
# --------------------------------------------------------------------------
# Whether to return a one-vs-rest (‘ovr’) decision function of shape
# (n_samples, n_classes) as all other classifiers, or the original
# one-vs-one (‘ovo’) decision function of libsvm which has shape
# (n_samples, n_classes * (n_classes - 1) / 2). However, note that
# internally, one-vs-one (‘ovo’) is always used as a multi-class strategy
# to train models; an ovr matrix is only constructed from the ovo matrix.
# The parameter is ignored for binary classification.
decision_function_shape="ovr",
# --------------------------------------------------------------------------
# Controls the pseudo random number generation for shuffling the data for
# probability estimates. Ignored when probability is False. Pass an int
# for reproducible output across multiple function calls.
random_state=None,
)
svc.fit(X, d)
svc.predict(X)
[3]:
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
[4]:
import numpy as np
plt.figure(figsize=(3.5, 3.5))
xx, yy = np.meshgrid(
np.arange(X[:, 0].min() - 1, X[:, 0].max() + 1, 1),
np.arange(X[:, 1].min() - 1, X[:, 1].max() + 1, 1),
)
zz = svc.predict(np.c_[xx.ravel(), yy.ravel()])
zz = zz.reshape(xx.shape)
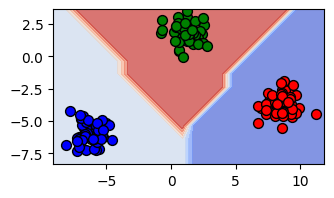
plt.contourf(xx, yy, zz, cmap=plt.cm.coolwarm, alpha=0.7)
plt.scatter(X[:50, 0], X[:50, 1], color="red", edgecolors="black", alpha=1.0, s=50)
plt.scatter(
X[50:100, 0], X[50:100, 1], color="blue", edgecolors="black", alpha=1.0, s=50
)
plt.scatter(X[100:, 0], X[100:, 1], color="green", edgecolors="black", alpha=1.0, s=50)
plt.gca().set_aspect("equal", adjustable="box")
plt.gca().set_xlim(xx.min(), xx.max())
plt.gca().set_ylim(yy.min(), yy.max())
plt.show()